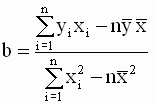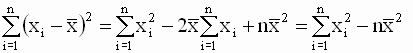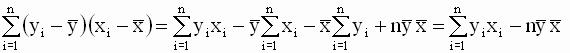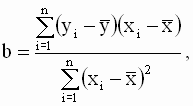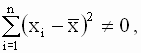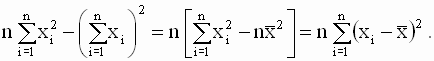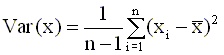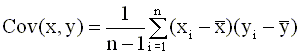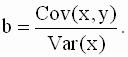|
2.2. Оценка параметров линейной модели по методу наименьших квадратов (МНК) В данном разделе рассматривается метод оценки параметров парной линейной регрессии, называемый методом наименьших квадратов (МНК). Метод наименьших квадратов имеет важнейшее значение во многих областях науки и техники, и применяется, как только возникает необходимость оценивания некоторых величин на основе статистической информации (эмпирических данных). Многие статистические процедуры оценки параметров как линейных, так и нелинейных моделей основаны на методе наименьших квадратов. Не преувеличивая можно сказать, что такие величайшие достижения, как запуск человека в Космос или посадка на Луну, стали возможны благодаря методу наименьших квадратов. Этот метод и многочисленные его модификации являются основными и в эконометрике. Поэтому при изучении данного курса ему нужно уделить особое внимание. 2.2.1. Критерий наименьших квадратов. Сравнение с другими возможными критериями Запишем уравнение для отдельных наблюдений (реализаций) в парной линейной регрессии
где t=1,2,…,n. Уравнение (2.5) выражает теоретическую связь
между зависимой y и независимой x
переменными в конкретных наблюдениях
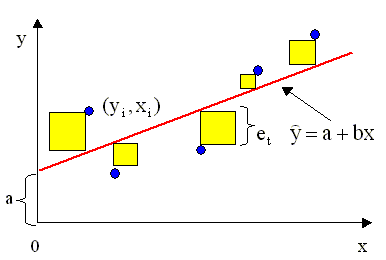
(см. рис. 2.1).
В это уравнение входят теоретические
значения параметров
где et - ошибки модели (другой, часто используемый в эконометрике термин - остатки модели). Очевидно, что Уравнение (2.6) выражает эмпирическую взаимосвязь между переменными модели и его можно записать только относительно конкретных наблюдений. Подчеркнем, что ошибки модели являются наблюдаемыми величинами, поскольку их можно определить исходя из наблюдений переменных модели. В методе наименьших квадратов оценки a и b параметров модели строятся так, что бы минимизировать сумму квадратов ошибок (остатков) модели по всем наблюдениям. Таким образом, критерий (целевая функция) наименьших квадратов записывается в виде
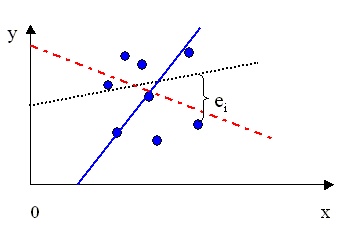
Очевидно, правая часть выражения (2.7) является квадратичной функцией параметров a и b. Замечание относительно переменных x. Отметим, что на этапе формулирования критерия наименьших квадратов нам не понадобились какие-либо дополнительные (ограничивающие) предположения относительно характера независимых переменных x модели - случайные они или детерминированные. При выводе уравнений для оценок эти предположения не имеют значения. Прежде чем переходить к формальному выводу уравнений для оценок, проиллюстрируем принцип метода наименьших квадратов графически. На рис 2.2. стороны квадратов равны ошибкам модели в каждом из наблюдений. Параметр a характеризует сдвиг линии относительно начала координат, параметр b - наклон этой линии относительно оси x. В методе наименьших квадратов оценки a и b истинных значений параметров выбираются так, чтобы сумма площадей квадратов была минимальна. Графическая иллюстрация принципа наименьших квадратов Замечание относительно выбора критерия - почему не другие критерии? Существует множество других критериев, которые в принципе можно использовать при построении эмпирических оценок параметров модели. Однако некоторые из них приводят к неоднозначным результатам и, несмотря на наглядность, не пригодны для использования. Например, почему бы не попытаться минимизировать просто сумму ошибок (остатков) модели, а не их квадратов. Очевидно, такой подход приводит к неоднозначному решению - можно бесконечным множеством способов провести прямую линию в плоскости (y,x) так, чтобы сумма остатков была равна нулю. При этом, как показано на рис. 2.3., между переменными y и x может вообще не существовать никакой зависимости. Другой, более приемлемый критерий - минимизировать сумму абсолютных величин остатков. Формально вывести выражения для оценок параметров с использованием этого критерия возможно, однако статистические свойства этих оценок и модели в целом установить сложно, поэтому данный критерий не получил широкого распространения. Существуют статистические критерии, такие, например, как критерий максимума правдоподобия (МП). Эти критерии требуют знания или определенных предположений относительно вида вероятностного распределения случайных составляющих модели. Подробный сравнительный анализ МНК и МП методов будет проведен в последующих разделах. 2.2.2. Вывод нормальных уравнений для оценок параметров регрессии. Решение нормальных уравнений. Варианты записи выражений для оценок параметров Получим выражения для оптимальных в смысле минимума МНК-критерия оценок параметров модели парной линейной регрессии. Согласно методу наименьших квадратов, необходимо минимизировать функцию двух переменных
по всем возможным значениям a и b при заданных (наблюдаемых) значениях x1,...,xn, y1,...,yn . Из курса высшей математики известно, что условием минимума функции вида (2.8) по переменным a и b является равенство нулю частных производных этой функции. Уравнения для определения оптимальных оценок получаются путем приравнивания нулю производной функции S(a,b) как функции только от a при фиксированном b и производной функции S(a,b) как функции только от b при фиксированном a. Это приводит к следующей системе уравнений: которую необходимо решить относительно переменных a и b. По правилам вычисления производных получим следующие выражения: так что значения параметров a и b, минимизирующие квадратичную форму (2.8), удовлетворяют соотношениям
После несложных преобразований эту систему можно записать в виде
Система уравнений (2.11), (2.12) называется системой нормальных уравнений для коэффициентов регрессии. Это система двух линейных уравнений с двумя неизвестными и она легко может быть решена, например, методом подстановки. Из первого уравнения системы находим:
где Подставив выражение для a во второе уравнение системы, получим
откуда
Таким образом, мы получили следующие соотношения для оценок параметров модели
Однако, в теоретических исследованиях и практических расчетах чаще используют другую, более удобную эквивалентную форму записи уравнений для оценок. Эта форма получается, если использовать следующие соотношения
Эти соотношения позволяют получить новую форму записи выражения для b (в отклонениях от выборочных средних значений)
которая вместе с выражением для a
дает решение задачи определения оптимальных оценок. Полученные оценки (независимо от формы записи) называют оценками наименьших квадратов. Заметим, что решение может существовать только при выполнении условия
которое означает, что определитель системы нормальных уравнений отличен от нуля. Действительно, этот определитель равен
Условие (2.15)
называется условием идентифицируемости
модели наблюдений Выражение для коэффициента b часто записывают также, используя понятия выборочной вариации (дисперсии) и выборочной ковариации. Выборочная вариация определяется соотношением вида
и выборочная ковариация следующим соотношением
Используя введенные понятия, формулу (2.13) для коэффициента b можно записать в виде
Замечание относительно выборочных дисперсии и ковариации. Напомним, что выборочная дисперсия характеризует степень разброса случайной величины относительно ее выборочного среднего значения. Выборочная ковариация характеризует степень линейной статистической взаимосвязи двух случайных величин. При определенных условиях, которые будут рассмотрены позже, выражения (2.16) и (2.17) являются несмещенными эмпирическими оценками теоретических дисперсии и ковариации. Иногда выборочные дисперсию и ковариацию определяют делением не на (n - 1), а на n. Такие оценки этих величин являются смещенными. Из выражения (2.18) видно, что значения b будут тем меньше, чем меньше ковариация между наблюдаемыми значениями переменных x и y и чем больше значения выборочной дисперсии Var(x) . Кроме того, знак b совпадает со знаком ковариации Cov(x,y), поскольку Var(x)>0. Замечание относительно полученных оценок. Оценки вида (2.13), (2.14) (или в других формах записи) являются выборочными эмпирическими оценками истинных (теоретических) параметров линейной регрессии. Эти оценки являются линейными относительно наблюдений. Эти оценки являются случайными величинами, поскольку зависят от случайных наблюдений. Если независимая переменная не случайная (детерминированная) величина, то ее дисперсия равна нулю, а ковариация детерминированной и случайной величин равна нулю. В этом случае выборочные дисперсия (вариация) x и выборочная ковариация величин x и y теряют смысл оценок соответствующих теоретических значений дисперсии и ковариации и должны рассматриваться только как некоторые характеристики наблюдаемых переменных, не связанные с их статистическими свойствами. И, наконец, подчеркнем еще раз, что уравнения для оценок получены без каких либо предположений относительно характеристик случайных составляющих модели. Интерпретация оценок параметров Определим оценку
Уравнение (2.19) определяет
эмпирическую регрессионную функцию,
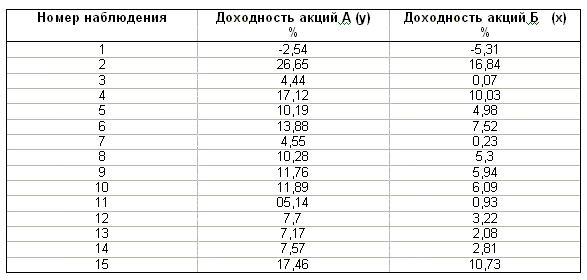
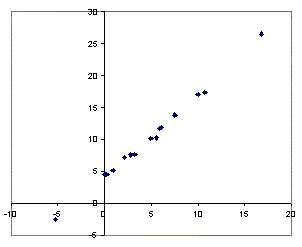
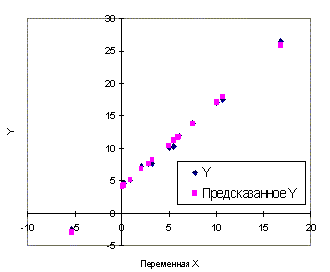
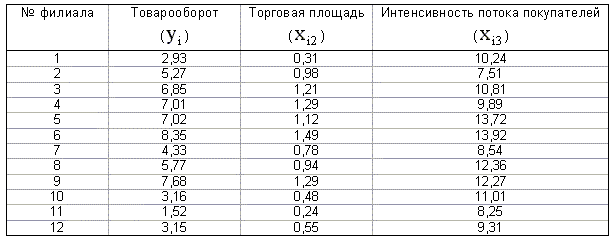
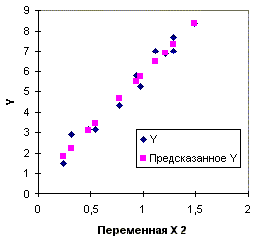
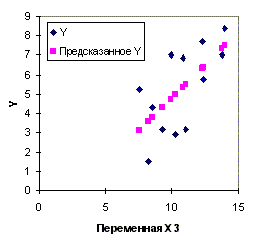
оценка Пример 2.1. Одним из ключевых понятий фондового рынка является понятие компании - лидера, изменение курса акций которой влияет на движение курсов акций других компаний данного сектора или отрасли экономики. Такое влияние может быть обусловлено технологической взаимосвязанностью компаний, однородностью выпускаемой продукции, монополизацией рынка и прочими причинами. Для количественного анализа влияния доходностей акций компании - лидера на доходности акций других компаний применяются методы регрессионного анализа. В таблице 1.1. приведены данные по годовым доходностям акций двух компаний А и Б, относящихся к одной отрасли (числовые данные из кн. Л.О. Бабешко, 2001. [4]). Построим модель парной регрессии для изучения зависимости доходности акций компании А от доходности акций компании Б. Из диаграммы рассеяния, построенной по этим данным (рис. 2.4a), можно предположить существование линейной зависимости между переменными y и x. Оценки параметров парной линейной регрессии, вычисленные по формулам (2.13), (2.14) равны: a=4,02; b=1,29. Уравнение регрессии имеет вид Оцененные значения зависимой переменной приведены на рис. 2.4б. Параметрам модели можно дать следующую интерпретацию. При x = 0 (доходность акций компании B равна нулю), ожидаемая (прогнозируемая) доходность акций компании A равна 4,02%. При увеличении доходности акций компании B на 1%, прогнозируемая доходность акций компании A вырастет на 1,29%. Таким образом, акции данной компании можно рассматривать как "агрессивные" по отношению к акциям компании B - оцененный коэффициент "бета" для них больше единицы. Пример 2.2. Торговое предприятие имеет несколько филиалов. Исследуем зависимость годового товарооборота отдельного филиала от: а) размера торговой площади; б) среднедневной интенсивности потока покупателей. Поскольку мы пока не умеем строить модели множественной регрессии, построим две "частные" модели парной регрессии. Таким образом, объясняемая переменная y - годовой товарооборот филиала (млн. руб.), объясняющая переменная в первой модели - размер торговой площади (тыс. кв. м.), обозначим ее x2, во второй модели - интенсивность потока покупателей (тыс. чел. в день), обозначим ее x3. Исходные данные для двенадцати филиалов приведены в таблице 1.2. (источник: Й. Грубер, 1996,[12]). На рис. 2.5а, 2.5б приведены диаграммы рассеяния для пар переменных (y, x2) и (y, x3). Оцененные значения коэффициентов первой регрессии: a=0,6057, b=5,2221. Ее уравнение имеет вид Для второй регрессии получаем следующие оценки: a=-2,0394, b=0,6846. Ее уравнение На рис. 2.5а, 2.5б приведены оцененные значения зависимой переменной (изображены в виде квадратов) в обеих регрессиях. Из этих рисунков видно, что переменная x2 ("торговая площадь") лучше объясняет поведение переменной y ("товарооборот"), чем переменная x3 ("среднедневная интенсивность покупателей"). Однако визуальное сравнение различных регрессий далеко не всегда позволяет оценить качество модели и выявить наилучшую из них. Поэтому в последующих разделах будут рассмотрены объективные критерии качества регрессионных моделей. Задание. Дайте интерпретацию параметров регрессий примера 2.2.
|
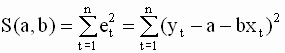
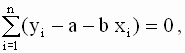
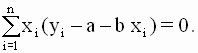
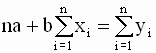
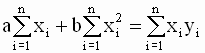
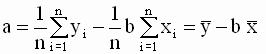
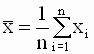 ,
, 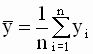 - выборочные
средние наблюдений.
- выборочные
средние наблюдений.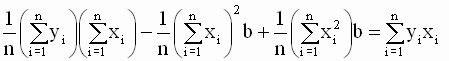 ,
,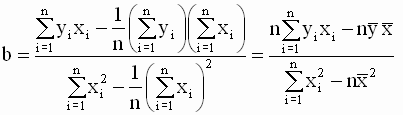 ,
,