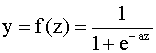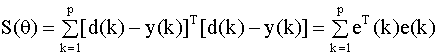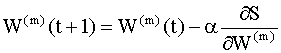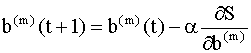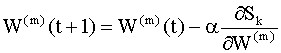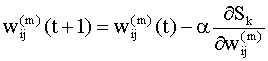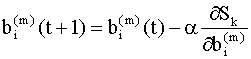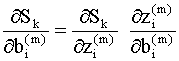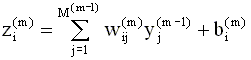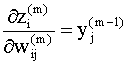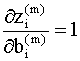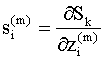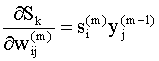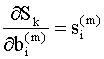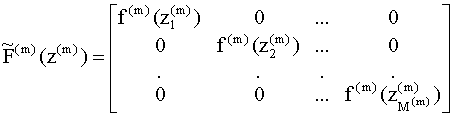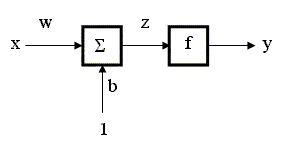
Эконометрика

Глава 9. ПРИМЕНЕНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ МОДЕЛИРОВАНИЯ В ЭКОНОМИКЕ

Данная глава учебника посвящена изложению методов построения нелинейных зависимостей на основе применения нейронных сетей. Это одно из наиболее быстро развивающихся нетрадиционных направлений эконометрики. На доступном уровне даны основные понятия теории нейронных сетей, математические модели нейронной сети, методы представления и аппроксимации данных с помощью нейронных сетей. Дан обзор применения нейросетевых моделей в экономике. Обсуждаются проблемы, связанные с построением и применением нейросетевых моделей.

9.1. Нейронная сеть как универсальный аппроксиматор нелинейных зависимостей

9.1.1. Модели нейронов. Архитектуры нейронных сетей

Нейронные сети - это самообучающиеся системы, имитирующие работу человеческого мозга.

Нейронные сети являются мощным инструментом анализа и аппроксимации зависимостей и широко используются в различных областях науки и техники, в том числе и в экономике. Нейронные сети эффективно используются на практике там, где необходимо решать задачи прогнозирования, классификации или управления. Широкое использование нейросетевого подхода обусловлено следующими причинами:

1) нейронная сеть способна обучаться на примерах в случаях, когда неизвестен вид и структура взаимосвязей между входными и выходными данными (зависимыми и независимыми переменными изучаемого процесса);

2) с помощью нейронных сетей можно получать приемлемое решение даже в случае неполной, искаженной и зашумленной информации;

3) нейронная сеть позволяет быстро обработать огромный объем информации и выявить в наблюдаемых данных скрытые закономерности;

4) с помощью нейронной сети можно аппроксимировать любую нелинейную зависимость.

Существует много типов нейронных сетей. Мы рассмотрим нейронную сеть, которая называется многослойным персептроном и представляет наиболее общую архитектуру нейронной сети, изучим основные элементы этой архитектуры и ее возможности в задачах аппроксимации различных нелинейных зависимостей. Таким образом, нейронные сети будут интересовать нас как математический аппарат, применяемый для аппроксимации неизвестных функций.

Модель нейрона с одним входом

Любая нейронная сеть состоит из сравнительно простых элементов - нейронов. Мы рассмотрим сначала модель нейрона с одним входом, а затем опишем общую модель со многими входами.

Искусственный нейрон (далее просто нейрон) с одним входом - это простой элемент, который умножает скалярный вход x на скалярный вес , формируя произведение . Затем полученная величина складывается с некоторой пороговой величиной , которая называется также смещением (bias). Величина определяет состояние или потенциал нейрона. Скалярный выход нейрона формируется как некоторая функция его состояния:

Функция f называется функцией активации (используются также термины: " переходная функция ", " решающая функция "). Вид функции активации выбирается разработчиком сети, в зависимости от особенностей конкретной задачи и назначения сети, а параметры нейрона и определяются в процессе обучения сети в соответствии с поставленной целью. Структура нейрона с одним входом показана на рис. 9.1.

Рис. 9.1. Нейрон с одним входом

Виды функций активации

Существуют различные виды функций активации:

1) линейные: выходной сигнал нейрона равен его состоянию (потенциалу);

2) ступенчатые: функция принимает два значения, что соответствует двум состояниям нейрона - активен/неактивен;

3) линейные с насыщением: выход нейрона принимает все значения в некотором интервале [a, b];

4) многопороговые: выход нейрона принимает одно из нескольких значений внутри интервала [a, b];

5) нелинейные функции с насыщением, так называемые сигмоидные (или лог-сигмоидные):

(9.1)

где коэффициент "a" определяет крутизну сигмоида. Эта функция активации принимает значения в промежутке (0, 1) при входных значениях, изменяющихся от до . Обычно параметр крутизны "a" учитывают путем выбора весов и порогов (через состояние z), и поэтому без потери общности полагают a = 1.

Существуют также и другие функции активации, такие как гауссовская, синусоидальная, всплесков и т.д.

На практике наибольшее распространение получила сигмоидная функция активации вида (9.1), во многом благодаря ее свойству дифференцируемости, что используется в наиболее известных алгоритмах обучения, таких как алгоритм обратного распространения ошибки (backpropagation).

Модель нейрона со многими входами

В общем случае нейрон может иметь более, чем один вход. Нейрон с N входами показан на рис. 9.2.

Рис. 9.2. Нейрон со многими входами

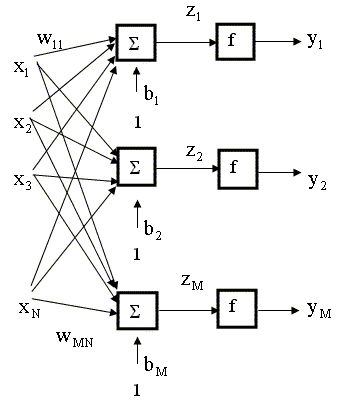
Каждый вход умножается на соответствующие весовые коэффициенты , (их называют также синаптическими коэффициентами или синаптическими весами) затем к получившемуся значению добавляется смещение . В результате состояние нейрона равно

(9.2)

Выражение (9.2) можно переписать в матричной форме

где , - весовая матрица (в случае одного нейрона она состоит из одной строки). Выход нейрона

Замечание об обозначениях

В обозначениях весовых коэффициентов нам понадобилось два индекса. Это связано с тем, что в дальнейшем мы будем рассматривать сети, состоящие из нескольких нейронов, каждый из которых имеет несколько входов со своими весами. Таким образом, первый индекс означает номер нейрона, которому соответствует весовой коэффициент в такой сети, второй индекс - номер входной переменной, которая умножается на данный коэффициент.

Архитектуры нейронных сетей

Нейронная сеть конструируется из совокупности нейронов, определенным образом связанных друг с другом и с внешней средой. Нейронные сети можно разделить на два вида:

1) статические или сети с прямой связью;

2) динамические или рекуррентные сети.

Мы будем рассматривать сети с прямой связью.

Такие сети состоят из статических нейронов, которые характеризуются тем, что сигналы на выходе нейронов появляются в тот же момент, когда подаются сигналы на вход. Таким образом, статическая сеть перерабатывает информацию без задержки, мгновенно. Архитектуры сетей могут быть различными. Типичная сеть состоит из нескольких слоев нейронов. Нейроны каждого слоя функционируют параллельно, выходы нейронов одного слоя являются входами для нейронов следующего слоя. Входные переменные поступают на нейроны входного (нижнего) слоя, выход сети формируется из выходов нейронов выходного (верхнего) слоя сети. Между входным и выходным слоями сети могут быть промежуточные, скрытые слои (иногда скрытыми слоями называют все слои, кроме выходного). Конкретный вид выполняемого сетью преобразования информации зависит как от характеристик нейронов, так и от ее топологии (количества нейронов в каждом слое и структуры связей между ними). Рассмотрим структуру отдельного слоя статической сети.

Слой нейронов

Сеть из одного слоя, состоящего из M нейронов, показана на рис. 9.3.

Рис. 9.3. Слой из M нейронов

Здесь каждый из N входов связан с каждым из нейронов, так что теперь матрица W имеет N столбцов. Каждый элемент входного вектора x умножается на соответствующий данному нейрону весовой коэффициент (элемент матрицы W). Каждый нейрон характеризуется смещением , состоянием (потенциалом) , функцией активации f и выходом (мы предполагаем, что все функции активации слоя имеют одинаковый вид, например, сигмоидные, но в общем случае они могут выбираться различными). Выходы нейронов слоя формируют вектор . В общем случае количество входов в слой не равно количеству нейронов в данном слое, то есть N не равно M. Входной вектор поступает в сеть после перемножения на весовую матрицу W:

(9.3)

В матрице весов (9.3) номер строки (первый индекс) совпадает с номером нейрона, которому соответствуют веса, формирующие данную строку (то есть, состояние данного нейрона определяется именно этими весами), номер столбца (второй индекс) совпадает с номером соответствующей входной переменной. Так, индексы у элемента означают, что этот весовой элемент соответствует третьему нейрону и на него умножается вторая входная переменная этого нейрона. Выходная переменная отдельного нейрона в слое равна

где - i - ая строка матрицы W.

Вектор выходных переменных слоя формируется в соответствии с правилом

где - вектор - функция, элементами которой являются M функций активации нейронов слоя, - вектор смещений.

Многослойная нейронная сеть

Рассмотрим сеть, состоящую из нескольких слоев. Каждый j - ый слой (j = 1, 2,...,P) характеризуется своей собственной весовой матрицей , вектором смещений , вектором состояния и вектором выходов , где верхний индекс означает номер слоя в сети. Таким образом, весовая матрица для первого слоя записывается как , для второго слоя - . На рис. 9.4 изображена сеть, состоящая из трех слоев (трехслойная сеть).

Рис. 9.4. Трехслойная нейронная сеть

Как видно из рисунка, сеть имеет N входов, нейронов в первом слое, - во втором и - в третьем, то есть различные слои имеют различное количество нейронов. Выходы первого и второго слоев являются соответственно входами второго и третьего слоев. Таким образом, второй слой можно рассматривать как однослойную сеть с количеством входов , количеством нейронов и весовой матрицей размерности. Входом второго слоя является вектор , а выходом - вектор .

Слой, выходы которого являются выходами сети, называется выходным слоем. Остальные слои называются скрытыми.

Нейронная сеть, изображенная на рис. 9.4, имеет два скрытых слоя (слои первый и второй) и третий выходной слой. Выходы первого слоя (и, соответственно, входы второго слоя) формируются по правилу

(9.4)

выходы второго слоя (и входы третьего)

(9.5)

выходы третьего слоя (и выход трехслойной сети)

(9.6)

Подставляя последовательно выражение (9.4) в (9.5), а (9.5) в (9.6), получим описание нейронной сети в виде суперпозиции трех функций:

9.1.2. Аппроксимация нелинейных зависимостей с помощью нейронных сетей

Двухслойная нейронная сеть с прямой связью, сигмоидными функциями активации в скрытом слое и линейными функциями активации в выходном слое обладает универсальными аппроксимирующими возможностями - является универсальным аппроксиматором. Это означает, что любую нелинейную функцию нескольких переменных можно сколь угодно точно аппроксимировать (приблизить) с помощью такой двухслойной нейронной сети, имея достаточно много нейронов в скрытом (входном) слое. К сожалению, не существует формального правила, позволяющего определить, сколько при этом необходимо иметь нейронов в скрытом слое, каковы должны быть веса входов и смещения, неизвестна также структура такой сети (ее топология) для данной конкретной задачи.

9.1.3. Понятие обучения и методы обучения нейронных сетей. Метод обратного распространения ошибки

Итак, мы теперь знаем, что нейронная сеть является универсальным аппроксиматором нелинейных функций (зависимостей). Если структура сети (ее топология) каким - либо образом выбрана, следующим шагом является разработка процедуры для настройки параметров (синаптических весов и порогов - смещений) сети данной структуры так, чтобы она наилучшим образом аппроксимировала изучаемую зависимость.

Процедура настройки (выбора) параметров нейронной сети называется тренировкой или обучением сети.

Мы рассмотрим наиболее распространенную и широко используемую на практике процедуру обучения нейронных сетей с прямой связью - так называемый алгоритм обратного распространения ошибки.

Как мы ранее установили, в сети, состоящей из нескольких слоев, выход одного слоя служит входом для последующего слоя сети (см. рис. 9.4). Взаимосвязь выходов и входов соседних слоев можно описать с помощью рекуррентных уравнений

(9.7)

для всех m =1,2,…,P-1, где P - количество слоев в сети. Входами нейронов первого слоя являются внешние входы в сеть, то есть . Это равенство служит начальным условием для уравнений (9.7). Выходы нейронов последнего (выходного) слоя являются выходами сети: . Уравнения (9.7) являются обобщением (9.4) - (9.6) на случай многослойной сети.

Обучение как оптимизация: критерий обучения

Обучение сети происходит следующим образом. "Учитель" имеет ряд примеров (образцов) правильного (желаемого) поведения нейронной сети:

(9.8)

где x(k) - вектор входов в сеть в k - ом примере, d(k) - желаемый выход сети ( образец) в k - ом примере, всего примеров p. На каждом шаге обучения на вход сети подается входной вектор x(k) и соответствующий ему выход сети сравнивается с образцом из множества (9.8). Результатом обучения сети является настройка (определение) ее параметров так, чтобы выход сети - вектор y(k) (ее реакция на предъявляемые входы из множества (9.8)) в каждом примере наилучшим образом (с минимальными отклонениями) аппроксимировал желаемое значение - вектор d(k). Критерием качества обучения обычно служит хорошо знакомый нам критерий наименьших квадратов. Для сети с одним выходом он имеет вид

(9.9)

здесь y(k) - скалярный выход сети, e(k) = d(k) - y(k) - ошибка аппроксимации в k - ом примере, - вектор неизвестных параметров сети (весов и смещений). Обобщая (9.9) на случай сети со многими выходами, можно записать

(9.10)

где y(k), d(k) и e(k) - векторы.

Алгоритм обратного распространения

Для минимизации критерия наименьших квадратов (9.10) используются численные итерационные методы поиска экстремумов (в нашем случае - минимума) нелинейных функций многих переменных, которые называются методами градиентного спуска (градиентными методами). Возможны два способа применения этих методов для оптимизации параметров нейронной сети. В первом из них берется градиент общей ошибки S, и параметры пересчитываются после предъявления всей совокупности обучающих примеров. Изменение параметров происходит в направлении наискорейшего спуска, то есть, в направлении, обратном направлению наибольшего изменения производной критерия качества, по следующему правилу:

Здесь - параметр алгоритма, который называется величиной градиентного шага или коэффициентом обучения.

Мы рассмотрим более подробно метод, который называется методом стохастической аппроксимации или методом стохастического градиента. В этом методе на каждой итерации параметры пересчитываются по правилу

(9.11)

(9.12)

где

Уравнения (9.11), (9.12) можно записать для каждого элемента матрицы весов и вектора смещений :

(9.13)

(9.14)

Что бы использовать итерационные правила (9.13), (9.14) в практических расчетах, необходимо уметь вычислять частные производные в правых частях этих соотношений. Эти производные легко вычислить, например, для однослойной сети с линейными функциями активации, так как в этом случае ошибку можно выразить в виде явной линейной функции весов сети. Если же сеть состоит из нескольких слоев, то для скрытых слоев ошибка будет неявной функцией весов, и в этом случае для вычисления частных производных можно использовать правило цепи. Используя правило вычисления производных неявных функций, можно записать

(9.15)

(9.16)

Второй сомножитель в каждом из этих выражений легко вычислить, поскольку состояния нейронов m - го слоя сети есть линейные функции весов и смещений в данном слое:

(9.17)

Имеем:

(9.18)

Определим чувствительность величины к изменению состояния i - го нейрона в слое m следующим образом:

(9.19)

(Вспомним, что производная характеризует скорость изменения функции при изменении аргумента на единицу, так что чем больше производная (9.19), тем функция более чувствительна к изменению аргумента). Используя (9.18), (9.19), уравнения (9.15) и (9.16) можно записать в виде

(9.20)

(9.21)

Учитывая (9.20), (9.21), итерационный алгоритм (9.13), (9.14) можно представить так

Переходя к матричной записи, получим

(9.22)

(9.23)

где и элементы этого вектора вычисляются по формулам (9.19). Далее, оказывается, что для вычисления чувствительностей в уравнениях (9.22), (9.23) можно использовать следующую рекуррентную схему:

(9.24)

(9.25)

где m = P-1,…,2, 1; - диагональная матрица вида

Используя рекуррентные соотношения (9.24), (9.25), можно вычислить чувствительности, как бы двигаясь в обратном направлении, от последнего слоя к первому. Отсюда и название алгоритма обучения - алгоритм обратного распространения.

9.1.4. Проблемы, связанные с построением нейронных сетей

Проблема переобучения и способность к обобщению

Ранее мы установили, что нейронная сеть является универсальным аппроксиматором, то есть для любой функции можно построить нейронную сеть, которая будет приближать эту функцию с заданной точностью. При этом открытым остался очень важный вопрос о том, сколько нейронов и слоев должна содержать такая сеть, и какова должна быть ее архитектура, чтобы степень приближения была адекватна решаемой практической задаче. Открытым также остался вопрос о необходимом количестве обучающих примеров, и то, каким образом их выбирать.

На первый взгляд кажется, что чем больше нейронов в сети и чем сложнее ее архитектура, тем лучше будет решена задача. Однако то, что является достоинством нейронных сетей, а именно, их способность очень точно приближать сложные нелинейные функции на обучающем множестве, может превратиться в недостаток, который заключается в неспособности делать обобщения при работе с реальными данными, не входящими в обучающее множество. Эта проблема называется переобучением.

Пусть обучающие данные порождаются следующей функцией

(9.26)

где x(k) - входной вектор, g - функция, которую мы хотим аппроксимировать сетью, d(k) - желаемый выход сети, u(k) - случайная составляющая (шум). Таким образом, сеть обучается на множестве наблюдаемых данных {d(k), x(k)}, k = 1, 2,…,p. Эффект переобучения проявляется в том, что на обучающем множестве переобученная сеть аппроксимирует неизвестную зависимость настолько точно, что повторяет все отклонения, вызванные случайными шумами, которые присутствуют в любых наблюдаемых данных, используемых для обучения сети. Поскольку шумы искажают вид действительной изучаемой зависимости, то и переобученная сеть будет моделировать не столько саму функцию g, сколько присутствующие в уравнении (9.26) шумы. Такая сеть не способна выявлять наиболее характерные, общие тенденции в изменении изучаемого явления и, следовательно, ее невозможно использовать для прогноза зависимой переменной.

Таким образом, при построении сети необходимо придерживаться следующего общего правила: сеть не должна быть слишком сложной и не должна слишком точно следовать данным из обучающего множества, но при этом она должна достаточно точно улавливать действительную структуру аппроксимируемой функции. Количество обучающих данных должно быть достаточным, что бы на их основе можно было адекватно выявить структуру изучаемой зависимости.

Существуют различные способы преодоления эффекта переобучения. Самый простой - увеличение количества примеров в обучающем множестве. При этом можно ожидать, что увеличение количества измерений будет приводить к уменьшению влияния шумов, по аналогии с моделями регрессии. Однако на практике, как правило, количество наблюдений ограничено, и такой подход трудно осуществить.

Другой способ заключается в следующем. Все множество наблюдений разбивается на два подмножества. Одно из них используется для обучения, другое, которое называется подтверждающим, для тестирования работы сети и обнаружения наступления момента переобучения. В процессе обучения сети вычисляется ошибка аппроксимации функции на подтверждающем множестве. Если она уменьшается, то это означает, что обучение улучшает характеристики сети и его необходимо продолжать. Если, начиная с некоторого момента, ошибка на подтверждающем множестве начинает возрастать, то это сигнализирует о том, что дальнейшее обучение приведет к переобучению, и, следовательно, процесс обучения необходимо прекратить. Такой метод называют методом ранней остановки. Его довольно просто реализовать на практике, если наблюдаемых данных достаточно и для обучающего, и для подтверждающего множеств. Недостатком данного метода является то, что не существует точного способа отбора элементов подтверждающего множества, тогда как конечный результат обучения сети существенно зависит от их выбора.

Другой способ улучшить способность сети к обобщению называется регуляризацией и заключается в следующем. В критерий качества обучения сети добавляется дополнительное слагаемое, которое штрафует сложность сети. В общем случае это слагаемое представляет собой сумму квадратов весовых коэффициентов сети и критерий имеет вид

где величина называется регуляризирующим параметром. Чем меньше веса в сети, тем больше она сглаживает наблюдаемые данные. Применение метода регуляризации приводит к некоторому ухудшению качества аппроксимации функции на обучающем множестве, но способность сети к обобщению, то есть к приближению функции за пределами этого множества, существенно возрастает. Проблема заключается в том, чтобы правильно выбрать значение регуляризирующего параметра . Если его значение слишком велико, то выход сети будет излишне сглаженным и сеть плохо приблизит функцию и наоборот, если выбрать слишком маленьким, то сеть будет переобучаться. Существуют различные формализованные методы выбора регуляризирующего параметра, которые мы здесь рассматривать не будем.

Вычислительные проблемы, связанные с поиском оптимальных весов

В предыдущем пункте мы установили, что задача обучения сети сводится, по существу, к поиску глобального минимума нелинейной функции многих переменных, для чего используются численные алгоритмы пошаговой оптимизации, реализующие метод наискорейшего спуска. При этом ключевыми проблемами являются: 1) выбор начального приближения для весов; 2) выбор величины шага. Эффективность работы алгоритмов обучения зависит от успешного решения данных проблем. Оптимизируемая функция в общем случае может иметь несколько локальных минимумов. Если выбрать шаг слишком маленьким, то скорость сходимости алгоритма (скорость обучения сети) будет низка и, кроме того, при этом велика вероятность попасть в локальный минимум. Если же шаг слишком большой, то алгоритм может проскочить глобальный минимум. Существуют различные модификации метода наискорейшего спуска (и основанного на нем алгоритма обратного распространения) в которых величина шага меняется в зависимости от этапа поиска минимума.

Выбор начального приближения также очень важен, так как от этого зависит, насколько быстро будет найден глобальный минимум и будет ли он найден вообще.

Более глубокое изучение и понимание подходов к решению этих проблем требует достаточно серьезных знаний в области вычислительной математики, которая является предметом, изучаемым разработчиками методов построения нейронных сетей и основанных на них нейросетевых пакетов программ. Пользователям же этих пакетов необходимо достаточно четко представлять "подводные камни", которые могут препятствовать успешному применению нейронных сетей на практике.