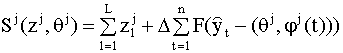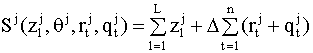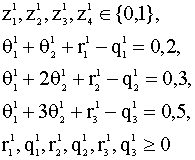|
В.В.
Домбровский - Эконометрика
Глава 8. АНАЛИЗ И ПРОГНОЗИРОВАНИЕ КОРОТКИХ ВРЕМЕННЫХ РЯДОВ С ПРИВЛЕЧЕНИЕМ ЭКСПЕРТНОЙ ИНФОРМАЦИИ 8.4. Способы оценивания адекватности трендовых моделей временного ряда по экспертным суждениям и выбора наилучшей модели 8.4.1. Общий подход к выбору наиболее адекватной модели При построении моделей коротких временных рядов статистические показатели адекватности модели, такие как коэффициент детерминации, дисперсии параметров и прогнозов, а также процедуры проверки гипотез относительно параметров и построения доверительных интервалов, становятся практически не работоспособными, поскольку на коротких выборках не возможно выявить статистические закономерности. Поэтому для выбора наиболее адекватной (наилучшей) модели временного ряда среди возможных моделей необходимо привлекать экспертную информацию. По - существу, в этом случае только экспертные суждения являются той доступной информацией, на основе которой можно выбрать наилучшую модель. Рассмотрим общий подход к решению задачи выбора наиболее адекватной модели с учетом экспертных суждений. Пусть имеется L экспертных суждений о поведении временного ряда на периоде упреждения, выраженных в виде неравенств (8.14). Предполагается также, что изучаемое явление может быть описано одной из N альтернативных трендовых моделей ряда, каждая из которых имеет вид
где Необходимо выбрать наиболее адекватную модель из множества моделей (8.39) с учетом наилучшего соответствия ее как экспертным суждениям, так и результатам наблюдений. Таким образом, мы имеем, по - существу, двухкритериальную задачу выбора: с одной стороны, модель должна удовлетворять максимально возможному для нее числу непротиворечивых элементарных высказываний (8.14), с другой - минимизировать суммарную ошибку аппроксимации наблюдаемых на периоде основания прогноза данных. Критерием, который учитывает два этих требования, может служить следующая функция:
где
системы неравенств (8.14), и равно нулю в противном случае. Малый множитель Для каждой модели решается
задача минимизации критерия (8.40) по
переменным
где 8.4.2. Выбор модели как решение задачи частично целочисленного линейного программирования В предыдущем пункте мы не конкретизировали вид функции F в критерии (8.40). Эта функция отвечает за соответствие модели наблюдаемым данным. Определим ее в виде Введем вспомогательные переменные
где t = 1, 2,…,n. Тогда задачу выбора наиболее адекватной модели можно сформулировать в виде следующей задачи частично целочисленного программирования: минимизировать линейную функцию
по переменным
Таким образом, процедура выбора наилучшей модели состоит из следующих шагов. 1) Для каждой модели согласно экспертным суждениям выписываем систему линейных неравенств вида (8.14). 2) Для
каждой j - ой модели решаем задачу
частично целочисленного линейного
программирования (8.42) - (8.46). В результате
находим оценки параметров моделей 3) Из
полученных на шаге 2) оптимальных
значений функций (8.44) перебором
определяем минимальное по всем j=1,
2,…,N значение функции считается наиболее адекватной среди рассматривавшихся N моделей. Пример 8.4 Набор данных состоит из трех наблюдений временного ряда: 0,2; 0,3; 0,5. Эксперты высказали три суждения: "значение временного ряда в момент t = 4 периода упреждения окажется не более 1 и не менее 0", "значение временного ряда в момент t = 6 периода упреждения окажется не более 1,5", "значение временного ряда в момент t = 8 периода упреждения окажется не менее 4". Необходимо сравнить три модели тренда
Таким образом, параметры
данной задачи равны: n = 3, m = 5, N = 3, Для выбора наилучшей из трех моделей (8.47) - (8.49) применим описанную выше процедуру. 1)
Выпишем ограничения вида (8.42) для модели (8.47)
Аналогичные системы неравенств выписываем и для моделей (8.48), (8.49). 2) Для
модели (8.47)
решаем задачу частично
целочисленного линейного
программирования вида:
минимизировать функцию при ограничениях (8.50) - (8.53) и дополнительных ограничениях вида
Решение задачи: Решение аналогичных задач для моделей (8.48) и (8.49) дает следующие результаты: 3)
Сравнивая значения критериев Задание Сформулируйте задачи частично целочисленного линейного программирования для моделей (8.48), (8.49).
|