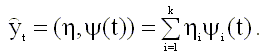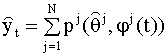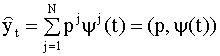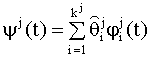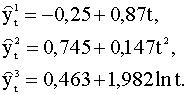|
В.В.
Домбровский - Эконометрика
Глава 8. АНАЛИЗ И ПРОГНОЗИРОВАНИЕ КОРОТКИХ ВРЕМЕННЫХ РЯДОВ С ПРИВЛЕЧЕНИЕМ ЭКСПЕРТНОЙ ИНФОРМАЦИИ 8.5. Методы комбинирования моделей и прогнозов Одним из способов повышения надежности и точности прогнозов является комбинирование различных моделей изучаемого ряда и прогнозов, полученных с помощью "частных" моделей. В случае коротких временных рядов при комбинировании моделей и прогнозов для оценки возможных значений временного ряда на периоде упреждения необходимо также привлекать экспертную информацию. Рассмотрим два возможных подхода к комбинированию моделей. Комбинирование моделей без предварительной оценки их параметров Пусть имеется N частных трендовых моделей временного ряда
Комбинированную модель получим как линейную комбинацию моделей вида (8.54)
где
где
Ограничения, представляющие экспертные высказывания для комбинированной модели, имеют вид
Оценки параметров модели определяются из условия минимума критерия
где F - строго выпуклая
функция параметров, при ограничениях (8.58). Если
комбинированная модель (8.57) согласована с
экспертными суждениями, то есть
система неравенств (8.58) совместна, то
существует единственное решение
задачи минимизации функции (8.59) при ограничениях (8.58).
Сформулированная задача аналогична
задаче построения трендовой модели с
учетом экспертных суждений,
рассмотренной в п. 8.3. Если в качестве
функции F выбрать квадратичную, то
имеем задачу квадратичного
программирования, если выбрать Прогноз значений ряда
строится по комбинированной модели (8.57), в
которой используются полученные
оценки вектора параметров Комбинирование моделей с предварительной оценкой их параметров Второй способ комбинирования моделей состоит в следующем. Сначала получают оценки параметров частных моделей вида (8.54). Частную модель с оцененными параметрами запишем в виде
Комбинированную модель получим как линейную комбинацию частных моделей вида (8.60)
Модель (8.61) можно записать в виде
где
при ограничениях, представляющих экспертные суждения, которые для комбинированной модели (8.62) имеют вид При непротиворечивых
экспертных суждениях решение данной
задачи существует и единственно.
Вычисленные оценки весовых
коэффициентов Выбрав функцию F в
критерии (8.64)
в виде Пример 8.5. Пусть имеются наблюдения ряда, равные 1; 1,3; 2; 3; 4,5. На основе анализа ряда для его описания выбраны три модели тренда, которые после оценки параметров имеют вид
Два эксперта высказали
следующие суждения: "значение
временного ряда в момент t = 6 периода
упреждения окажется в интервале [5, 7]",
"значение временного ряда в момент t
= 7 периода упреждения окажется не
более 9". В данном примере n = 5, N
= 3, Используя второй подход, построим комбинированный прогноз временного ряда на периоде упреждения m = 2. По формуле (8.63) вычислим векторы
Система неравенств, соответствующая экспертным суждениям, имеет вид
Задача линейного программирования формулируется следующим образом: минимизировать линейную функцию при ограничениях (8.65) - (8.67) и дополнительных ограничениях вида
В результате решения данной задачи получаем оценки весов комбинированной модели Используя полученные
значения весов, вычисляем прогноз по
комбинированной модели (8.62):
|
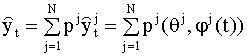
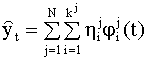
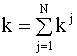 и вектор функцию
и вектор функцию