|
5.4. Анализ стационарных временных рядов 5.4.1. Определения и основные характеристики стационарных временных рядов. Эргодические ряды В предыдущем разделе мы установили, что после исключения из наблюдаемых значений ряда систематических не случайных компонент, соответствующих тренду и сезонным колебаниям, остается ряд случайных остатков. В настоящем разделе мы будем изучать случайные ряды, предполагая, что неслучайные компоненты ряда исключены (впрочем, возможно, что они и вообще отсутствуют в наблюдаемом первоначально ряде). Таким образом, мы не будем делать смыслового различия между случайными рядами, получившимися после выделения не случайной составляющей и рядами, в которых эта составляющая изначально отсутствует. Такие ряды могут состоять из взаимно коррелированных членов и иметь довольно сложную параметрическую структуру. Нашей задачей является построение моделей таких рядов и их оценка (идентификация). При этом мы ограничимся классом стационарных рядов, который и будем изучать. Пусть Говорят, что ряд является стационарным в узком смысле (или строго стационарным), если функция распределения F не зависит от момента t при любых целых k > 0, то есть для любых целых k, t, m. Таким образом, если ряд строго стационарный, то любые k последовательных членов ряда имеют одинаковое совместное распределение независимо от их положения в ряде. Очевидно, что в этом случае отдельные члены ряда тоже распределены одинаково. Не зависят от времени и основные статистические характеристики случайных членов стационарного ряда: математическое ожидание
дисперсия
ковариация
Говорят, что временной ряд является стационарным в широком смысле, если для его членов выполнены только условия (5.37), (5.38), то есть среднее и дисперсия членов ряда постоянны. Ковариация между любыми двумя членами одного и того же ряда называется автоковариацией. Таким образом, соотношения (5.39) определяют автоковариацию. Соответственно, можно определить и автокорреляцию
где Совокупность коэффициентов Заметим, что коэффициент Характеристики стационарного ряда, вообще говоря, можно оценить, имея достаточно большое количество его реализаций. Например, если бы была возможность получить достаточное количество наблюдений хотя бы одного члена ряда yt в какой - либо один и тот же фиксированный момент времени t, то можно рассчитать выборочные среднее и дисперсию ряда, используя обычные определения выборочных оценок. Однако при этом возникает проблема, связанная с тем что, как правило, на практике особенно при изучении социально - экономических явлений в распоряжении исследователя имеется только одна наблюдаемая реализация ряда. К счастью, существует широкий класс стационарных случайных рядов, называемых эргодическими, для которых выборочные характеристики можно определить по наблюдениям только одной реализации ряда. Пусть известна некоторая
конкретная реализация стационарного
случайного ряда
Согласно
теореме Биргхофа - Хинчина [см. М.
Кендалл, А. Стьюарт], среднее по
времени
то есть
среднее по времени
Процессы, для которых
выполнено условие (5.41) и второй момент (дисперсия)
Для эргодических рядов имеет место следующее обобщение теоремы Биргкофа - Хинчина: пусть ряд эргодический, тогда для почти всех реализаций автокорреляция равна корреляции, вычисленной по реализации, то есть
Теорема Биргкофа - Хинчина и ее обобщение имеют фундаментальное значение для практики, так как позволяют оценивать среднее, дисперсию и автокорреляции по единственной наблюдаемой реализации случайной последовательности. Это означает, что для оценок этих величин можно использовать следующие выборочные значения: оценка среднего
оценка дисперсии (несмещенная)
оценка автоковариации
оценка автокорреляции
Требование эргодичности процесса не является слишком ограничивающим. В частности, оно выполняется, если автокорреляция убывает до нуля по мере удаления друг от друга соответствующих членов ряда (это следует из условия (5.42)). В данном разделе мы рассмотрим модели автокоррелированных стационарных временных рядов, которые называются моделями авторегрессии (или авторегрессионными моделями). С простейшей моделью такого типа, а именно, с моделью авторегрессии первого порядка мы сталкивались при изучении регрессионных моделей с коррелированными остатками (см. п. 4.4). Модели авторегрессии получили широкое применение на практике. Модель авторегрессии первого порядка Простейшая модель автокоррелированного стационарного ряда, которая часто используется на практике, имеет вид
где u - случайная величина с
нулевым средним, величины ui
и uj некоррелированы
между собой при Модель (5.47) называется моделью авторегрессии первого порядка (сокращенно пишут АР(1) - модель). Рассмотрим свойства этой модели. Очевидно, что Далее, подставляя последовательно в уравнение (5.47) выражение для y на предыдущем шаге, получим
Таким образом, имеем
Из уравнения (5.48) получаем, что среднее дисперсия
Числовой ряд в выражении (5.49) сходится,
если
Замечание При выводе выражения (5.50) для
дисперсии ряда (5.47)
существенным было условие, что
дисперсия ряда будет равна бесконечности и ряд не будет эргодическим. Условие Из уравнения (5.48) следует, что yt зависит от случайных величин ut, ut - 1, ut - 2,..., но не зависит от будущих значений ut + 1, ut + 2,... С учетом этого можно записать откуда имеем и, следовательно, корреляция между членами yt и yt + 1 равна
Аналогично для автокорреляции k-го порядка получаем откуда будем иметь Свойство эргодичности
процесса авторегрессии позволяет
использовать формулы (5.43) - (5.46) для выборочных
оценок его дисперсии и параметра
где s02 - оценка
дисперсии Задание Определите оценки параметров авторегрессии по методу наименьших квадратов. Убедитесь, что они совпадут с (5.51). Модель авторегрессии второго порядка (АР(2) - модель) Модель авторегрессии второго порядка записывается в виде
где относительно последовательности u сохраняются сделанные ранее предположения. Ряд, описываемый уравнением (5.52) называется рядом Юла. Прежде всего, отметим, что yt зависит только от настоящего и прошлых значений случайной последовательности u и не зависит от ее будущих значений. Умножим уравнение (5.52) на yt - 1 и yt - 2 и возьмем математическое ожидание, получим
Разделив правые и левые части
уравнений (5.53),
(5.54) на
Решая систему (5.55), (5.56) относительно
параметров
Получим соотношение, связывающее коэффициенты автокорреляции модели и дисперсию случайной составляющей u. Для этого умножим обе части уравнения авторегрессии (5.52) на yt и применим операцию взятия математического ожидания. Получим откуда
Полученные выражения для
коэффициентов регрессии можно
использовать для идентификации
модели, если ряд (5.52)
эргодический. Для этого, так же как при
оценивании авторегрессии первого
порядка, автокорреляции Определим условия, при
которых ряд (5.52)
будет эргодическим. Для этого выразим
коэффициенты автокорреляции через
коэффициенты авторегрессии
Вспоминая, что коэффициенты
автокорреляции должны удовлетворять
условиям
которые можно записать в виде
Соотношения (5.62) дают необходимые и достаточные условия эргодичности ряда (5.52). Замечание Условия (5.62) можно получить в терминах решений характеристического уравнения модели авторегрессии. Для модели второго порядка оно записывается в виде
Условия (5.62) эквивалентны требованию, что бы все корни характеристического уравнения (5.63) (среди них могут быть как действительные, так и комплексно-сопряженные) лежали вне единичного круга. Модель авторегрессии порядка p (АР(p) - модель) Рассмотрим теперь ряды, которые являются обобщением рядов, рассмотренных выше, и описываются уравнением
или
Процесс, описываемый уравнением (5.65) называется процессом (рядом) авторегрессии порядка p (авторегрессионным рядом, процессом авторегрессии p-го порядка). Для того, что бы процесс авторегрессии порядка p удовлетворял условиям эргодичности, необходимо и достаточно, чтобы корни его характеристического уравнения лежали вне единичного круга. Если хотя бы один из корней лежит внутри такого круга, то эволюция членов ряда носит взрывной характер - значения членов ряда будут неограниченно и быстро возрастать. Замечание Иногда вместо (5.64) авторегрессионный ряд удобнее представлять в виде или
где
Необходимым и достаточным условием эргодичности процесса (5.66) является требование, чтобы все корни уравнения (5.67) лежали внутри единичного круга. Подчеркнем, что модели вида (5.65) и (5.66) не имеют принципиальных различий, они эквивалентны с точностью до знаков входящих в них членов ряда. Не трудно установить, что yt зависит от настоящего и прошлого значений ut, ut - 1,.., и не зависит от будущих значений ut + 1, ut+ 2,... Получим соотношения для автокорреляций процесса АР(p). Для этого умножим правую и левую части уравнения (5.64) на yt - k (k > 0) и применим к обеим частям получившегося уравнения операцию взятия математического ожидания. Получим соотношение разделив которое на
Система уравнений (5.68) называется системой Юла-Уокера и
ее можно использовать для
идентификации модели. Действительно,
учитывая, что
или в векторно-матричной форме
где
Решение системы (5.69) существует, если матрица R невырождена, и его можно записать в виде Для получения выборочных
оценок параметров авторегрессии в
этом уравнении истинные значения
автоковариаций Замечание 1. Аналогичная схема оценивания параметров авторегрессии получается, если минимизировать критерий суммы квадратов ошибок (МНК)
то есть задачу оценивания можно решать так же как в случае многомерной линейной регрессии. Замечание 2. Поскольку задача оценивания параметров авторегрессии по существу аналогична оцениванию параметров множественной линейной регрессии по методу наименьших квадратов, то и свойства оценок будут аналогичны: несмещенность, состоятельность, эффективность. Кроме того, для проверки адекватности авторегрессионных моделей можно использовать тесты, разработанные для моделей множественной регрессии. Оценку дисперсии откуда, разделив на Выборочная оценка s02 получается путем замены величин, стоящих в правой части, их выборочными оценками. Замечание 3. Если в уравнении (5.68) положить последовательно k=p+1, p+2,… , то получаем рекуррентное соотношение, которое можно использовать для вычисления автокорреляций процесса авторегрессии в произвольный момент, зная их p первых значения. Выбор порядка авторегрессионной модели Прежде всего, отметим, что на практике редко используются модели порядка больше двух. Для того, чтобы адекватно установить порядок авторегрессионной зависимости, можно рассчитать характеристики процесса, которые называются частными автокорреляциями ( частными автокорреляционными функциями). Введем понятие частной автокорреляции (частной автокорреляционной функции). Частные автокорреляции отражают степень статистической (линейной) зависимости (корреляции) между наблюдениями yt и yt - k, когда влияние на yt промежуточных членов ряда yt -1, yt - 2,..., yt – k + 1 устранено. Частная автокорреляция модели авторегрессии первого порядка Рассмотрим модель ряда, описываемую уравнением (5.47). Частная автокорреляция, отражающая зависимость членов ряда yt и yt - 2 при исключении влияния промежуточного значения yt - 1, определяется по формуле
где Для авторегрессии первого порядка все частные автокорреляции равны нулю. Это означает, что в такой модели значение yt зависит только от предыдущего члена yt - 1. Такие процессы называются Марковскими. Итак, для того, чтобы убедиться, что анализируемый ряд действительно описывается моделью авторегрессии первого порядка, необходимо вычислить частный коэффициент корреляции, используя выборочные оценки автокорреляций. Если он статистически незначимо отличается от нуля, то на самом деле наблюдаемый ряд укладывается в схему авторегрессии первого порядка. Частные автокорреляции модели авторегрессии второго порядка (ряд Юла) Рассмотрим модель ряда, описываемую уравнением (5.52). В соответствии с формулой (5.71) частная корреляция между yt и yt- 2 равна
или, используя выражения (5.60), (5.61) для Можно показать, что частные корреляции более высоких порядков (то есть частные корреляции между компонентами ряда, отстоящими друг от друга более чем на два такта), равны нулю. Обобщая рассмотренные
примеры, можно сделать вывод о том, что
для процесса авторегрессии порядка p
частные корреляции порядка p (то
есть корреляции между членами yt
и yt - p при устранении
влияния промежуточных членов), будут
равны последнему коэффициенту Для установления порядка модели можно использовать упрощенный подход, который заключается в следующем. Предполагая, что анализируемый процесс действительно является процессом авторегрессии, последовательно увеличиваем порядок регрессии до тех пор, пока сумма квадратов ошибок (5.70) не перестанет ощутимо (в пределах заданной точности) уменьшаться. 5.4.3. Модели скользящего среднего В разделе 5.3.2 при решении задачи выделения тренда случайного процесса мы использовали метод скользящих средних, когда процесс в некоторой точке представлялся в виде взвешенной суммы наблюдений ряда в соседних точках. При рассмотрении процессов авторегрессии, в частности, модели первого порядка АР(1) мы получили представление случайного процесса в виде (см. п. 5.4.2, формула (5.48))
что по существу также является моделью скользящих средних по бесконечному числу значений белого шума. В связи с этим, рассмотрим процесс скользящих средних, который в общем виде определяется формулой
где усреднение проводится по
бесконечному числу точек. Отметим, что
ряд (5.72) в
общем случае не будет эргодическим, но
он будет таковым, если ряд
На практике при моделировании реальных рядов используют конечное число слагаемых в модели скользящих средних, то есть частные случаи общей модели (5.72). Такие модели имеют вид
Модель вида (5.73) называется моделью скользящего среднего порядка q (сокращенно - СС(q) - модель). Если yt -
стационарный ряд, ряд скользящих
средних vt будет также
стационарным, причем при любых
значениях параметров Рассмотрим ряд скользящих средних вида
здесь ut - последовательность некоррелированных случайных величин ("белый шум") с нулевым средним. Поступая стандартным образом, можно получить выражение для автокорреляций ряда (5.74), которые равны
Таким образом, автокорреляции процесса скользящего среднего порядка q равны нулю для всех j больше q. Этот факт используется на практике при подборе порядка модели по наблюдаемым данным. Идентификация (оценивание) модели (5.74) проводится с использованием теоретических соотношений (5.75). Общая схема построения оценок параметров аналогична той, которая применялась при оценивании моделей авторегрессии и состоит из следующих шагов: 1) по
наблюдениям вычисляем выборочные
оценки 2)
используя формулу (5.75) составляем систему q
уравнений относительно q неизвестных
параметров 3) решаем полученную систему уравнений относительно неизвестных параметров и получаем их оценки. К сожалению, в отличие от задачи оценивания параметров уравнений авторегрессии, когда получалась система линейных уравнений относительно неизвестных (система Юла-Уокера (5.68)), система уравнений для определения параметров моделей скользящего среднего всегда будет нелинейной. Это порождает весьма сложные проблемы, связанные с необходимостью применения итерационных численных методов решения систем нелинейных уравнений и возможностью существования неединственного решения. Пример: процесс скользящего среднего первого порядка В качестве примера рассмотрим процесс скользящего среднего первого порядка
где для удобства второй член
взят со знаком минус. В модели (5.76)
оцениванию подлежит единственный
параметр
Оценивание параметра
Данное уравнение имеет два
корня, причем согласно теореме Виета,
произведение этих корней равно
свободному члену, то есть единице. В
качестве оценки параметра
Нетрудно заметить, что
разложение (5.77)
есть ни что иное, как представление
процесса скользящего среднего в виде
процесса авторегрессии с бесконечным
числом членов (бесконечного порядка).
При При Понятие обратимости играет важную роль в теории процессов авторегрессии и скользящего среднего и может быть обобщено на общий случай СС(q) процессов. Замечание Формулу (5.77) нетрудно получить, записав уравнение (5.76) в виде
и подставляя последовательно в уравнение (5.78) выражение для u на предыдущем шаге (аналогичный прием использовался при выводе формулы (5.48)). Задание Выпишите систему уравнений для оценивания параметров СС(2) модели. 5.4.4. Модели авторегрессии - скользящего среднего Более полное и точное название рассматриваемого в данном разделе класса моделей - модели авторегрессии со скользящими средними в качестве ошибок. Данные модели являются естественным обобщением рассмотренных выше моделей авторегрессии и скользящих средних. В моделях авторегрессии предполагалось, что остаточный член представляет собой независимую (некоррелированную) случайную последовательность типа белого шума. Однако на практике более адекватными для описания ошибок в модели авторегрессии могут оказаться модели типа скользящего среднего. В связи с этим рассмотрим смешанную модель, включающую как авторегрессионную составляющую, так и скользящие средние. Такая модель имеет вид
Процесс, описываемый моделью вида (5.79) называется процессом авторегрессии - скользящего среднего, или сокращенно АРСС(p,q). Замечание Иногда вместо (5.79) для процесса авторегрессии - скользящего среднего удобнее использовать несколько другую запись
где Отметим основные, принципиальные моменты, касающиеся анализа и оценивания АРСС(p,q) моделей. 1). Текущие значения ряда yt не зависят от будущих значений ошибок. В этом нетрудно убедится, последовательно (бесконечное число раз) подставляя в уравнение (5.79) выражения для yt - 1, yt - 2,..., по той же формуле (5.79). Аналогичную схему мы использовали неоднократно ранее при анализе АР(p) и СС(q) процессов. 2). Процесс авторегрессии - скользящего среднего вида (5.79) будет стационарным (а в нашем случае и эргодическим) тогда и только тогда, когда стационарным является процесс авторегрессии вида
где лежали вне единичного круга (по модулю были больше единицы). 3). Процесс авторегрессии - скользящего среднего будет обратимым, если таковым является процесс скользящего среднего вида где лежали вне единичного круга (по модулю были больше единицы). Напомним, что условие обратимости обеспечивает физическую реализуемость процесса. 4). Автокорреляции АРСС(p,q) - процессов получаются по той же схеме, как и ранее для АР(p), СС(q) - процессов. Сначала получаем уравнения для автоковариаций, умножив правую и левую части уравнения (5.79) на yt - k и применяя к обеим частям получившегося уравнения операцию математического ожидания:
где для всех 5). Процедуры определения оценок параметров АРСС(p,q) - модели носят итерационный характер и включают этап численного решения системы нелинейных уравнений. Один из возможных подходов к идентификации АРСС(p,q) моделей мы рассмотрим позже в главе 6 в рамках теории смешанных регрессионно-авторегрессионных процессов. В заключение отметим, что АР(p) и СС(q) - процессы являются частными случаями АРСС(p,q) - процесса. Формулируя цели анализа временных рядов (см. п. 5.2), в качестве одной из основных целей мы выделили прогнозирование поведения изучаемого явления (системы) на некоторый будущий период времени. Правильный (достоверный) прогноз поведения системы в будущем - необходимое условие обоснованного принятия решения в настоящем. Проблема прогнозирования - это сложная комплексная задача, и поэтому неудивительно, что вопросам прогнозирования, в частности в экономике, посвящено громадное количество исследований. Можно выделить два подхода к данной задаче. Первый подход заключается в следующем. На основе наблюдений прошлого поведения процесса (явления) строится подходящая модель ряда (например, авторегрессионная). При этом предполагается, что данная модель адекватно отражает поведение процесса как в прошлом, так и в будущем. Исходя из этого предположения, пытаются экстраполировать прошлое поведение ряда на будущее. Этот подход безусловно имеет право на существование и оправдал себя на практике, так как часто вся информация, которую мы имеем об экономической системе, представлена лишь в виде некоторого временного ряда, описывающего внешние тенденции поведения системы, а для того, чтобы построить более сложную модель самой системы, отражающую внутренние связи и описывающую ее структуру (построить феноменологическую модель) система недостаточно изучена, а иногда отсутствует даже принципиальная возможность такого изучения (по крайней мере, на данном этапе развития экономической науки и общества). Таким образом, подход к прогнозированию экономических показателей, основанный на анализе временных рядов, использует следующие фундаментальные предпосылки: 1) модель ряда адекватно отражает истинное поведение системы; 2) механизмы, определяющие поведение системы, не меняются, так что будущее поведение системы определяется ее прошлым поведением. При использовании такого подхода проблема состоит в том, что с течением времени механизм изучаемого явления не остается неизменным, в результате меняются не только параметры уравнений модели, но и структура самих уравнений. Поэтому данный подход можно использовать при прогнозировании лишь на небольшие промежутки времени (выполнять краткосрочные, в некоторых случаях среднесрочные прогнозы). Второй подход основан на построении феноменологической модели системы, которая описывала бы структуру системы, отражала внутренние связи, влияние внешних факторов. Такие модели существенно более сложны, их построение требует глубокого изучения механизма явления, существенно большей информации о системе, оценивание их параметров - сложная задача. Естественно, что любой прогноз должен основываться на достоверной, постоянно обновляющейся информации, модели должны постоянно корректироваться в соответствии с новыми данными. При прогнозировании поведения реальных процессов не следует ограничиваться каким - либо одним методом, необходимо пользоваться любыми доступными формальными (использующими математический инструментарий) и не формальными способами прогнозирования, проводить анализ и сравнение полученных результатов, привлекать экспертную информацию. Прогнозирование на основе моделей авторегрессии Рассмотрим более подробно
прогнозирование на основе моделей
авторегрессии. Будем предполагать,
что выделены систематические
компоненты анализируемого процесса (такие
как тренд, сезонные колебания),
оставшийся после этого АР(p) процесс
идентифицирован - определены его
порядок и оценки параметров. В теории
прогнозирования известен следующий фундаментальный
результат: наилучшим в смысле
минимума среднеквадратичной ошибки
линейным прогнозом случайной
последовательности yt в
момент времени t на Основываясь на этом утверждении, мы легко можем построить прогноз ряда по модели авторегрессии. Пример: прогноз процесса авторегрессии первого порядка Пусть процесс описывается уравнением
Прогноз на один шаг равен Здесь мы воспользовались свойством марковости процесса авторегрессии первого порядка (5.83) - текущее значение процесса зависит только от его значения в предыдущий момент (см. п. 5.4.2). Прогноз на два шага равен Аналогично получаем прогноз
на Пример: прогноз процесса авторегрессии второго порядка Пусть процесс описывается уравнением В этой модели текущее значение ряда зависит от двух предыдущих. Прогноз на один шаг будет равен Прогноз на два шага Прогноз на Используя методы регрессионного анализа можно построить доверительные интервалы для прогнозов. Рассмотренные примеры можно обобщить на случай процессов авторегрессии произвольного порядка. Методы прогнозирования процессов более сложной структуры будут рассмотрены в главе 6.
|
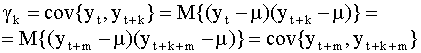
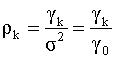
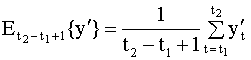
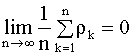
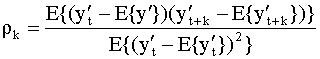
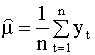
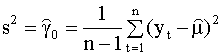
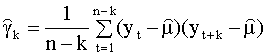
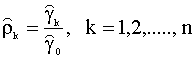
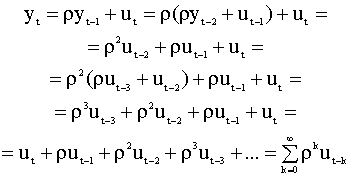
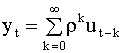
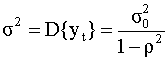
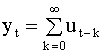
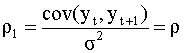
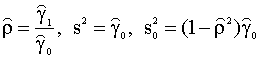
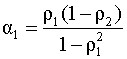
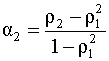
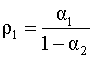
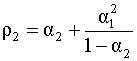
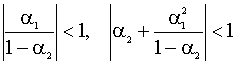
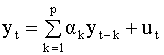
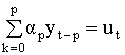
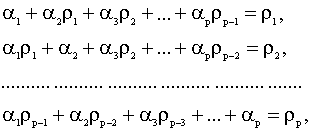
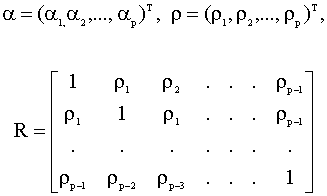
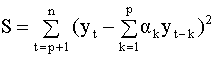
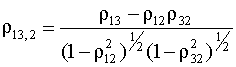
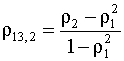
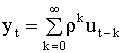
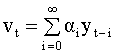
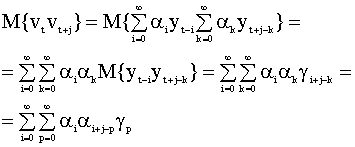
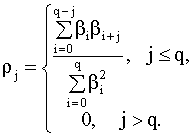
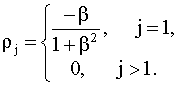
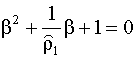
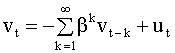
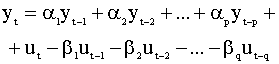
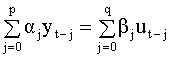
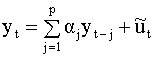
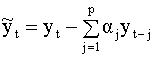 . Для обратимости
СС(q) процесса необходимо и достаточно,
чтобы корни его характеристического
уравнения
. Для обратимости
СС(q) процесса необходимо и достаточно,
чтобы корни его характеристического
уравнения




