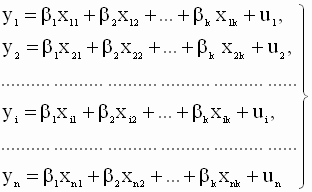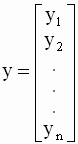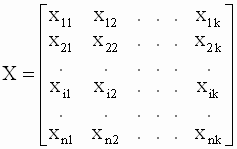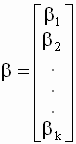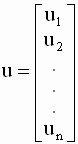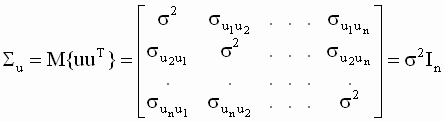Эконометрика

Глава 3. МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ

Цель данной главы - дать достаточно полное изложение материала, необходимого для изучения основных вопросов, связанных с построением моделей классической множественной линейной регрессии. Основное внимание уделяется проблемам оценки параметров, проверки адекватности и достоверности моделей.

3.1. Модель множественной линейной регрессии: содержательная интерпретация и предпосылки

Модель множественной линейной регрессии (или коротко - множественная линейная регрессия) предназначена для проверки и изучения связи (объяснения поведения) между одной зависимой переменной (эндогенной) и несколькими независимыми (экзогенными) переменными. Предполагается, что такая связь теоретически может быть описана (специфицирована) линейной зависимостью (функцией) вида:

(3.1)

где Y - зависимая (объясняемая, эндогенная) переменная - регрессанд, U - случайная составляющая модели, x_j - независимые (объясняющие, экзогенные) переменные - регрессоры.

Очевидно, что модель множественной линейной регрессии является обобщением модели парной линейной регрессии на многомерный случай.

В данном разделе мы будем рассматривать классическую модель множественной линейной регрессии. Это означает, что независимые переменные (регрессоры) предполагаются не случайными (детерминированными) величинами. Обобщения данной модели на случай, когда эта предпосылка не выполняется, будут рассмотрены в последующих разделах.

Модель (3.1) связывает зависимую и независимые переменные в отдельных наблюдениях (реализациях) переменных

(3.2)

Переменные y и u в уравнении (3.2) являются реализациями случайных величин Y и U. Отметим, что единственным источником неопределенности (случайности) в уравнениях (3.1) и (3.2) является случайная составляющая модели U. Переменная x₁ = x_i1 = 1 (для всех i=1,2,…n) и называется вспомогательной переменной для свободного члена. Она вводится для удобства записи уравнений многомерной линейной регрессии. Таким образом, коэффициент регрессии в уравнениях (3.1), (3.2) является свободным членом, который называется также параметром сдвига.

Для статистической оценки параметров регрессионной модели необходим набор (множество) данных наблюдений зависимой и независимых переменных. Эти данные могут быть пространственными - в этом случае наблюдаются различные объекты, но наблюдения относятся к одному и тому же моменту или периоду времени. Данные могут быть представлены в виде временных рядов наблюдений зависимой (объясняемой) и независимых (объясняющих) переменных - в этом случае наблюдается поведение одного объекта в различные (но одинаковые для всех переменных) моменты времени. Для каждого из этих наблюдений согласно линейной модели можно записать уравнения

(3.3)

Запись уравнений с использованием векторов и матриц

Данную систему уравнений удобно записать в векторно-матричном виде. Для этого введем следующие обозначения:

вектор - столбец (столбцовая матрица) наблюдений зависимой переменной (регрессанда)

матрица наблюдений независимых переменных (регрессоров)

вектор - столбец коэффициентов (параметров)

вектор - столбец реализаций случайной составляющей в отдельных наблюдениях

Таким образом, здесь y - вектор - столбец размерности n, элементы которого - наблюдения зависимой переменной (регрессанда); X - матрица размерности (n x k), ее столбцы содержат наблюдения независимых переменных (регрессоров), i-ый столбец матрицы X (кроме первого) содержит n наблюдений i - го регрессора, первый столбец этой матрицы состоит из единиц; - вектор - столбец размерности k, его элементы - коэффициенты уравнения регрессии; u - вектор - столбец размерности n, его элементы - реализации случайной составляющей модели в каждом наблюдении.

С использованием введенных обозначений, систему (3.3) из n уравнений можно записать более компактно

(3.4)

Отметим, что матричная форма записи уравнений линейной регрессии существенно проще и, как мы увидим в дальнейшем, ее использование позволяет получить и записать многие результаты для оценок в компактном виде. Основные правила действий с матрицами и векторами, которые необходимо при этом знать, приведены в приложении.

Предпосылки классической многомерной линейной регрессионной модели

Сформулируем предпосылки, которые необходимы при выводе формул для оценок параметров модели, изучения их свойств и тестирования качества модели. Эти предпосылки обобщают и дополняют основные предпосылки классической модели парной линейной регрессии (условия Гаусса-Маркова), но часть из них существенны именно для многомерной модели.

Предпосылка 1. Независимые переменные не случайны и измеряются без ошибок. Это означает, что матрица наблюдений X - детерминированная.

Предпосылка 2. (первое условие Гаусса-Маркова) Математическое ожидание случайной составляющей в каждом наблюдении равно нулю

Предпосылка 3. (второе условие Гаусса-Маркова) Теоретическая дисперсия случайной составляющей одинакова для всех наблюдений

Напомним, что это свойство случайной составляющей называется гомоскедастичностью.

Предпосылка 4. (третье условие Гаусса-Маркова) Случайные составляющие модели некоррелированы для различных наблюдений. Это означает, что теоретическая ковариация

Предпосылки 3,4 можно записать, используя векторные обозначения

здесь , причем (это означает, что - симметричная матрица), I_n - единичная матрица размерности n (напомним, что единичная матрица - это квадратная матрица, у которой по диагонали стоят элементы, равные единице, а остальные равны нулю), верхний индекс T - означает транспонирование. Матрица называется теоретической матрицей ковариаций(или ковариационной матрицей).

Предпосылка 5. (четвертое условие Гаусса-Маркова). Случайная составляющая и объясняющие переменные некоррелированы (для модели нормальной регрессии это условие означает и независимость). В предположении, что объясняющие переменные не случайные, эта предпосылка в классической регрессионной модели всегда выполняется.

Предпосылка 6. Коэффициенты регрессии - постоянные величины.

Предпосылка 7. Уравнение регрессии идентифицируемо. Это означает, что параметры уравнения в принципе оцениваемы. Или, другими словами, решение задачи оценивания параметров существует и единственно.

Предпосылка 8. Регрессоры не коллинеарны. В этом случае матрица наблюдений регрессоров должна быть полного ранга (ее столбцы должны быть линейно независимы). Данная предпосылка тесно связана с предыдущей, так как при применении для оценивания коэффициентов регрессии метода наименьших квадратов ее выполнение гарантирует идентифицируемость модели (если количество наблюдений больше количества оцениваемых параметров).

Предпосылка 9. Количество наблюдений больше количества оцениваемых параметров, то есть n>k.

Все эти предпосылки одинаково важны, и только при их выполнении можно применять классическую регрессионную модель на практике.

Предпосылка о нормальности случайной составляющей. При построении доверительных интервалов для коэффициентов модели и прогнозов зависимой переменной, проверке статистических гипотез относительно коэффициентов, построении процедур для анализа адекватности (качества) модели в целом необходимо дополнительное предположение о нормальном распределении случайной составляющей. С учетом этой предпосылки модель (3.1) называется классической линейной многомерной нормальной моделью регрессии.

В эмпирических социально-экономических исследованиях сформулированные предпосылки далеко не всегда выполняются. При их нарушении необходимо строить так называемые обобщенные модели линейной регрессии, которые будут рассмотрены в последующих разделах. При изучении регрессионных моделей и, особенно, при применении их на практике очень важно (в решающей степени) понимать роль и значение этих предпосылок. От того, на сколько корректно (правильно) и осознанно используются возможности регрессионного анализа, зависит успех всего эконометрического моделирования и, в конечном счете, обоснованность принимаемых решений.

Рассмотрим ряд понятий, связанных с моделью многомерной линейной регрессии.

Математическое ожидание регрессанда

С учетом предпосылки 1 в линейной функции регрессии случайными являются только переменные U, относительно которых выполнена предпосылка 2. Применяя к обеим частям уравнения (3.2) оператор математического ожидания, получим

(3.5)

Математическое ожидание (3.5) регрессанда определяет систематическую часть уравнения регрессии (регрессанда).

Эмпирическая линейная функция регрессии

Систематическая часть уравнения регрессии, в которой вместо теоретических значений параметров стоят некоторые их оценки, называется эмпирической линейной функцией регрессии.

Эмпирическая функция регрессии записывается в виде

(3.6)

где коэффициенты b_j, (j=1,2,…,k) - оценки теоретических значений параметров модели. Переменная является точечным прогнозом зависимой переменной Y при некоторых заданных значениях независимых переменных (регрессоров). Эмпирическая линейная регрессионная функция определяет регрессионную гиперплоскость в линейном k-мерном пространстве.

Ошибки (остатки) регрессионного уравнения

Разность

(3.7)

называется ошибкой (остатком) уравнения в i-ом наблюдении.

Ошибки являются вычисляемыми величинами и поэтому их можно считать известными при каждом фиксированном наборе наблюдений и заданных значениях параметров модели. Очевидно, величины ошибок (при фиксированных наблюдениях) зависят только от выбора коэффициентов b, которые являются оценками истинных (теоретических) значений коэффициентов . Чем точнее оценки, тем, вообще говоря, меньше остатки модели (при условии ее правильной спецификации), тем лучше данная модель соответствует наблюдаемой выборке, и тем лучше модель "настроена" именно на данную выборку. Оценки параметров классической многомерной линейной модели чаще всего строятся с использованием обычного (классического) многомерного метода наименьших квадратов.