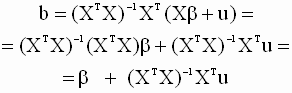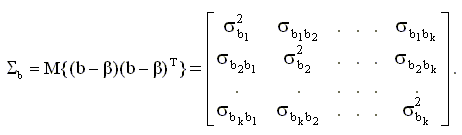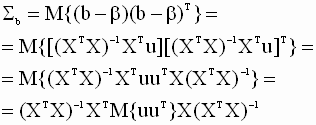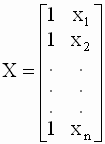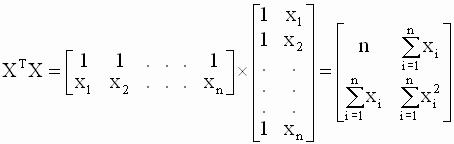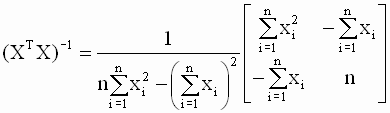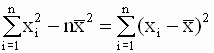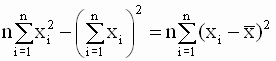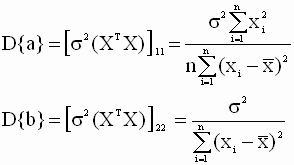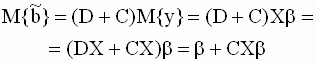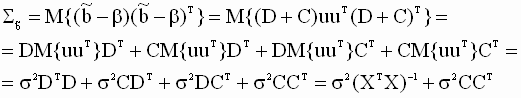Эконометрика

Глава 3. МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ

3.3. Статистические свойства оценок параметров линейной модели множественной регрессии. Теорема Гаусса-Маркова

МНК - оценки параметров регрессии b_j (j=1,2,…,k), определяемые по формуле (3.15) являются, очевидно, линейными функциями наблюдений зависимой переменной y, и, следовательно, относятся к классу линейных оценок. Поскольку наблюдения являются реализациями случайной переменной Y, то и оценки являются реализациями случайных величин. В классической регрессионной модели при заданной матрице регрессоров X свойства вектора случайных составляющих модели u определяют статистические свойства вектора зависимых переменных y и, следовательно, статистические свойства оценок b как случайных величин. В многомерной регрессии мы имеем дело с векторными случайными величинами. Важными характеристиками векторной случайной величины является ее математическое ожидание и ковариационная матрица, диагональные элементы которой - дисперсии компонент случайного вектора. Получим выражения для этих характеристик вектора оценок b.

Математическое ожидание вектора оценок. Несмещенность оценки

Подставим в формулу (3.15) для оценки вместо вектора y его выражение (подчеркнем, что здесь мы рассматриваем y и u как случайные величины (векторные), а не конкретные их реализации). Получим

(3.21)

Применяя к обеим частям данного выражения оператор математического ожидания, и вспоминая, что (X^TX)^-1 (X^TX)=I_k , и, в силу предпосылки 2, M{u}=0, а также учитывая, что в классической модели истинные значения параметров и матрица регрессоров X - неслучайны (предпосылка 1), получим

(3.22)

Таким образом, в классической многомерной линейной модели регрессии оценки коэффициентов, полученные по методу наименьших квадратов, являются несмещенными, то есть .

Истинная ковариационная матрица вектора оценок. Эффективность оценки

Истинная ковариационная матрица оценок коэффициентов

Получим выражение для истинной ковариационной матрицы вектора оценок. Ковариационная матрица вектора b по определению равна

(3.23)

Эта матрица служит важной характеристикой полученных МНК - оценок коэффициентов регрессии. Ее диагональные элементы определяют теоретические дисперсии оценок отдельных коэффициентов. Ее элементы , стоящие вне главной диагонали, равны ковариациям оценок. Заметим, что , то есть - симметричная матрица.

Из выражения (3.21) получаем

(3.24)

Подставляя выражение (3.24) в (3.23), будем иметь

(3.25)

где мы учли, что (X^TX)^-1 - симметричная матрица. Далее, в силу предпосылки 3 ковариационную матрицу вектора возмущений можно представить в виде

(3.26)

где I_n - единичная матрица размерности n. Подставляя (3.26) в (3.25), получаем

или, окончательно имеем

(3.27)

Диагональные элементы ковариационной матрицы являются дисперсиями соответствующих МНК - оценок коэффициентов множественной регрессии.

Замечание. Вывод формул для дисперсий коэффициентов парной линейной регрессии.

Из общей формулы (3.27) можно легко получить формулы (2.22), (2.23) для дисперсий коэффициентов парной линейной регрессии, которые ранее были даны без вывода в главе 2 (см. п. 2.3.3.). Действительно, в случае парной регрессии матрица наблюдений регрессоров X имеет вид

Матрица

и обратная к ней матрица

Задание.

Убедитесь, что приведенное выше выражение для (X^TX)^-1 действительно определяет матрицу, обратную к матрице (X^TX) .

Ранее (см. п. 2.2.2.) мы показали, что имеет место равенство

Умножим обе его части на n, получим

Учитывая это равенство, выпишем уравнения для диагональных элементов ковариационной матрицы в случае парной регрессии, которые и будут дисперсиями соответствующих коэффициентов

Нетрудно убедиться, что полученные формулы совпадают с формулами (2.22), (2.23).

Эффективность оценок

Покажем, что оценка наименьших квадратов является эффективной, то есть наилучшей в смысле минимума дисперсий компонент вектора оценок b.

Рассмотрим некоторый вектор линейных несмещенных оценок коэффициентов регрессионной модели, отличный от вектора оптимальных оценок b. Его можно записать в виде , где D=(X^TX)^-1X^T ; C - некоторая матрица. Математическое ожидание вектора равно

Поскольку оценка несмещенная, то должно выполнятся равенство CX = 0, и, следовательно, CD^T= 0 и DC^T= 0 . С учетом этого, ковариационная матрица вектора оценок равна

Таким образом, мы получили, что

Далее, поскольку матрица (неотрицательно определенная), то имеет место неравенство

откуда следуют аналогичные неравенства и для диагональных элементов ковариационных матриц, которые являются дисперсиями соответствующих коэффициентов модели

Это и доказывает эффективность МНК-оценок.

Полученные результаты можно сформулировать в виде теоремы.

Теорема Гаусса-Маркова Оценка вида (3.15) параметров классической многомерной линейной регрессии по методу наименьших квадратов является наилучшей (эффективной) линейной несмещенной оценкой (Best Linear Unbiased Estimator, BLUE).

Состоятельность оценок

Свойство состоятельности заключается в том, что матрица ковариаций вектора оценок должна стремится к нулевой матрице при увеличении числа наблюдений. Условие состоятельности можно сформулировать в терминах собственных значений матрицы (X^TX), а именно, для состоятельности МНК - оценок необходимо и достаточно, чтобы наименьшее собственное значение этой матрицы стремилось к нулю при количестве наблюдений n, стремящемся к бесконечности. Существуют и другие формулировки условий состоятельности МНК - оценок.