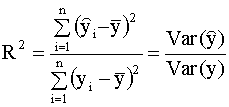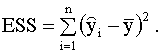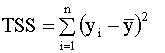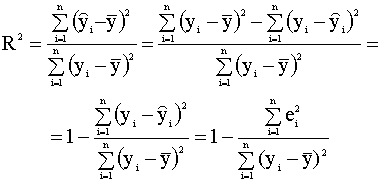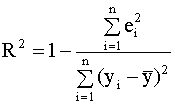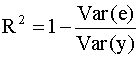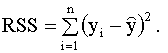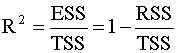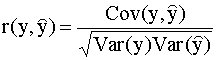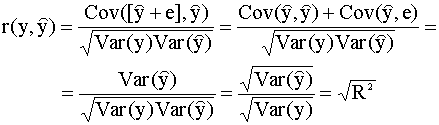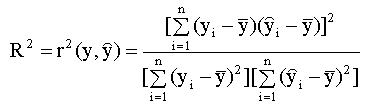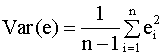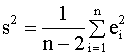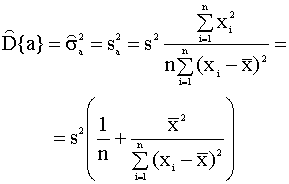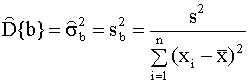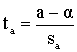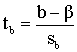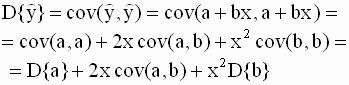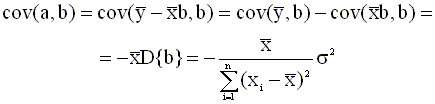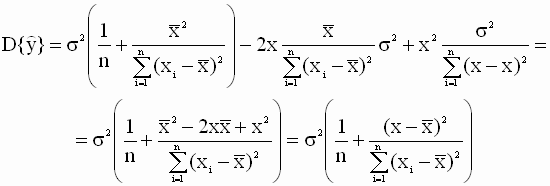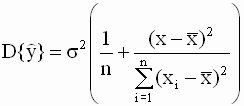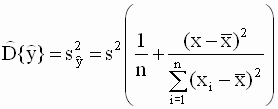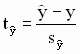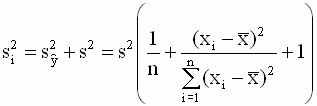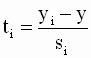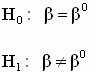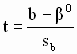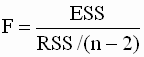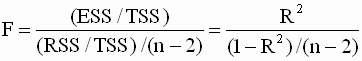|
2.4. Проверка адекватности регрессионной модели 2.4.1. Коэффициент детерминации В классическом регрессионном анализе предполагается, что функция регрессии известна (специфицирована) с точностью до параметров, то есть набор регрессоров (независимых переменных) определен. В эмпирических исследованиях экономических и социальных процессов, из множества возможных вариантов регрессионных уравнений, которые отличаются набором регрессоров, необходимо выбрать наиболее адекватную модель (регрессионную функцию). Такая модель наилучшим образом объясняет поведение реального процесса. Для оценки качества модели линейной регрессии в классическом регрессионном анализе используется показатель, который называется коэффициентом детерминации R2 (читается R - квадрат). Коэффициент детерминации играет важную роль в регрессионном анализе. Ниже приведены три эквивалентных определения этого показателя, которые отличаются формой записи и способом интерпретации. Представим отклонение зависимой переменной от ее выборочного среднего в виде где первое слагаемое - это отклонение значения зависимой переменной в i-ом наблюдении от прогноза ее среднего значения, второе слагаемое - отклонение прогноза среднего значения зависимой переменной от ее выборочного среднего. Возводя обе части последнего равенства в квадрат и суммируя левые и правые части полученного выражения, запишем:
Рассмотрим последнее слагаемое в правой части этого выражения. Имеем:
Далее, вспоминая доказанные в п. 2.3.2 свойства остатков (соотношения (2.20), (2.21))
получим, что
и, таким образом, окончательно можем записать
Сумму, стоящую в левой части этого выражения, называют полной суммой квадратов, первая сумма в правой части (2.25) называется суммой квадратов, объясненной моделью, вторая сумма правой части называется остаточной суммой квадратов. Далее, используя выражение (2.25), можно записать
поскольку,
Здесь мы использовали следующие соотношения:
(это следует из первого
уравнения системы нормальных
уравнений (2.11), (2.12), Первое представление коэффициента детерминации Определим коэффициент детерминации следующим соотношением
Заметим, что в числителе выражения (2.27) стоит сумма квадратов, объясненная моделью (explained sum of squares), будем использовать для ее обозначения аббревиатуру ESS, так что
В знаменателе стоит полная сумма квадратов (total sum of squares), для ее обозначения будем использовать аббревиатуру TSS, так что
Выражению (2.27) можно дать следующую интерпретацию: это доля общей вариации зависимой переменной, объясненная линейной регрессией. Второе представление коэффициента детерминации Используя разложение (2.25) , можно записать
так что
или
Формула (2.28) (или эквивалентная ей формула (2.29)) дает вторую форму представления коэффициента детерминации. Обозначим остаточную сумму квадратов
Тогда можно записать соотношение которое представляет собой разложение полной суммы квадратов на сумму квадратов, объясненную моделью, и остаточную сумму квадратов. Используя эти три суммы, можно записать также, что
Таким образом, значение коэффициента детерминации тем выше, чем больше доля объясненной моделью суммы квадратов ESS по отношению к полной сумме квадратов TSS. Термины «полная» и «объясненная
моделью» суммы квадратов имеют
следующий смысл. Полная сумма
квадратов TSS = RSS в ситуации, когда b
= 0 и «наилучшая» прямая имеет вид Третье представление коэффициента детерминации Введем понятие коэффициента корреляции
между фактическим значением
переменной y и ее прогнозом
Коэффициент корреляции Используя правила действий с выборочными вариациями и ковариациями (см. п. 2.3.2), нетрудно видеть, что
Здесь мы использовали также
следующее соотношение: Таким образом, мы получили третье выражение для коэффициента детерминации:
Замечание. Отметим, что минимизация суммы квадратов остатков (МНК-критерий) эквивалентна максимизации коэффициента детерминации. Действительно,
и, таким образом, минимизация суммы квадратов остатков приводит к максимизации коэффициента R2 в выражении (2.29). Практическая рекомендация. При построении модели парной линейной регрессии следует добиваться, чтобы значение коэффициента детерминации было как можно ближе к единице. Для его вычисления проще и удобнее использовать формулу (2.28). Пример 2.4. Вычисление коэффициента детерминации для модели примера 2.1. Вычисления по формуле (2.28) дают следующее значение коэффициента детерминации для модели примера 2.1: R2 = 0,9965. Таким образом, коэффициент детерминации близок к единице, что указывает на хорошее качество аппроксимации наблюдаемых данных построенной моделью. Пример 2.5. Вычисление коэффициентов детерминации для моделей товарооборота филиалов примера 2.2. Для первой регрессии примера 2.2., описывающей зависимость товарооборота от торговой площади, коэффициент детерминации R12 = 0,96886. Для второй регрессии, описывающей зависимость товарооборота от среднедневной интенсивности потока покупателей R22 = 0,42433. Таким образом, полученные объективные показатели качества регрессионных моделей - коэффициенты детерминации, подтверждают сделанное ранее предположение (см. пример 2.2) о том, что первая регрессия лучше объясняет поведение зависимой переменной. 2.4.2. Построение доверительных интервалов для коэффициентов регрессии Рассмотренный в предыдущем разделе показатель адекватности - коэффициент детерминации используется для оценки качества регрессионных моделей в целом, при сравнении альтернативных моделей. В данном разделе рассматриваются процедуры, позволяющие сделать вывод о качестве оценок истинных значений отдельных параметров уравнения. Оценки дисперсий МНК-оценок коэффициентов Одной из важных
характеристик качества оценки
является ее дисперсия, как мера
отклонения относительно ожидаемого
значения. Полученные ранее уравнения (2.22), (2.23) (или
(2.24))
для дисперсий оценок зависят от
неизвестной дисперсии
Выражение (2.30) используется для
вычисления оценок дисперсий оценок a
и b коэффициентов регрессии. Для
этого в уравнениях (2.22), (2.23), (2.24) теоретическая
дисперсия
Определение доверительных интервалов оценок параметров модели Полученные оценки параметров
t-тесты основаны на следующем важном утверждении: случайные переменные
подчиняются центральному распределению Стьюдента (t-распределению, отсюда название - t - тесты) с (n-2) степенями свободы. Замечание относительно степеней свободы. Количество степеней свободы равно количеству наблюдений переменных минус количество оцениваемых коэффициентов модели. В модели парной линейной регрессии таких коэффициентов всего два. Увеличение количества коэффициентов в модели регрессии при фиксированном размере выборки соответственно уменьшает количество степеней свободы. Очевидно, что погрешности
точечных оценок коэффициентов равны
соответственно
где Соотношения (2.35), (2.36) можно переписать в виде
Интерпретация доверительных интервалов. Выражения (2.37), (2.38) интерпретируются
следующим образом: величина Эти интервалы называются доверительными интервалами. Доверительные интервалы называют также интервальными оценками и они дополняют точечные оценки параметров. Интервальные оценки дают дополнительную, ценную информацию о надежности точечных оценок и позволяют повысить надежность суждений о точечных оценках. Определение доверительных интервалов. Для определения
доверительных интервалов
используются t - статистики
Стьюдента вида (2.33),
(2.34). Для
статистики t (имеющей t-распределение)
можно определить значение (из таблицы t-критерия)
Подставляя в (2.39) вместо t
выражения статистик (2.33) и (2.34) и разрешая
неравенства относительно параметров
Таким образом, двусторонние симметричные доверительные интервалы с вероятностью Можно сказать, что при 95% - ом уровне доверия доверительный интервал в среднем в 95 случаях из 100 накрывает истинное значение параметра, при 99% - ом - в 99 случаях из ста. Пример 2.6. Определение
доверительных интервалов для модели
примера 2.1. Определим границы
доверительных интервалов для
коэффициентов модели примера 2.1. Будем
предполагать, что регрессор x - не
случайная величина. Тогда оценки
дисперсий остатков и коэффициентов
регрессии вычисляются по формулам (2.30), (2.31), (2.32). Они
равны соответственно: Пример 2.7. Доверительные
интервалы для моделей примера 2.2.
Аналогично предыдущему примеру, можно
определить границы доверительных
интервалов для двух регрессий примера
2.2. Критическое значение t -
статистики при уровне значимости 0,05
и p = 12 - 2 = 10 степеней свободы равно 2,228.
Оцененные среднеквадратичные
отклонения оценок коэффициентов
первой регрессии равны sa = 0,2887,
sb = 0,2961. Доверительные
интервалы для коэффициентов: Задание. Постройте доверительные
интервалы для моделей примеров 2.1, 2.2.
при уровне значимости 2.4.3. Точечный и интервальный прогноз зависимой переменной Определим прогноз среднего значения зависимой переменной как оценку теоретической взаимосвязи с помощью эмпирической (оцененной) регрессионной функции
где x - некоторое значение
независимой переменной, вообще говоря,
несовпадающее со значениями
переменных из выборки, по которой
оценены параметры регрессии.
Поскольку оценки a и b -
случайные величины, то и прогноз Замечание. Прогноз среднего значения и прогноз индивидуального значения зависимой переменной. Следует различать прогноз среднего значения регрессанда как оценку его математического ожидания с учетом предпосылки M(ui) = 0 (первого условия Гаусса - Маркова), и прогноз как оценку возможного индивидуального значения (реализации) yi регрессанда y. В этом случае в уравнение (2.42) следовало бы добавить прогноз случайной составляющей модели. В качестве прогнозного значения случайной составляющей берут ее математическое ожидание, которое равно нулю. Это различие в понимании смысла прогноза существенно, так как соответствующие дисперсии ошибок прогноза и доверительные интервалы будут различны. Рассмотрим сначала прогноз среднего зависимой переменной. Дисперсия прогноза среднего зависимой переменной и ее оценка При выводе уравнений для дисперсии и ее оценки мы будем использовать правила преобразования теоретических вариаций (дисперсий) и ковариаций случайных величин. Эти правила такие же как и для соответствующих выборочных характеристик, которые были установлены в разделе 2.3.2. Для записи теоретических значений вариаций и ковариаций мы будем использовать обозначения var( , ), cov( , ). Получим выражение для дисперсии прогноза. Имеем
где взаимная ковариация имеет вид
Подставляя в (2.43) выражения (2.22), (2.23) для дисперсий оценок параметров и взаимной ковариации (2.44), получим
Таким образом, окончательно имеем
Обратим внимание, что в
выражении (2.45)
переменная x - это значение
регрессора (независимой переменной),
для которого определяется прогноз
среднего значения зависимой
переменной (регрессанда). Поскольку в (2.45)
теоретическое значение дисперсии
случайной составляющей модели
Определение доверительных интервалов для прогноза среднего значения зависимой переменной Определим доверительный
интервал для прогноза (2.42) зависимой
переменной. Этот интервал с
вероятностью
и его границы вычисляются по следующим формулам: нижняя граница верхняя граница Доверительный
интервал для отдельных значений
зависимой переменной (значений в
отдельных наблюдениях,
индивидуальных значений) Дисперсия отдельных наблюдений зависимой переменной и ее оценка Определим дисперсию наблюдаемых значений зависимой переменной Очевидно, что Заменяя в (2.47) неизвестные
теоретические значения дисперсий
Доверительный интервал для индивидуальных значений зависимой переменной Доверительный интервал для индивидуальных значений строится с использованием t-статистики вида
Границы интервала, с
вероятностью нижняя граница верхняя граница где количество степеней свободы p = n-2. Пример 2.8. Доверительные границы прогнозов среднего и индивидуального значений зависимой переменной в модели примера 2.1. Определим прогноз доходности акций компании для момента t = 3, то есть для значения x = x3 = 0,07 и построим доверительные интервалы прогнозов среднего и индивидуального значений, предполагая, что регрессор x - не случайная величина. Используя уравнение регрессии с оцененными коэффициентами (см. пример 1.1.), получим Для определения
доверительных интервалов необходимо
предварительно вычислить оценки
дисперсий прогноза среднего и
индивидуального значений зависимой
переменной. Используя формулы (2.46) и (2.47),
соответственно получим: нижняя верхняя Доверительные границы индивидуального значения: нижняя верхняя Задание. Постройте интервальные прогнозы средних и индивидуальных значений зависимой переменной для регрессий примера 2.2. 2.4.4. Проверка статистических гипотез относительно коэффициентов регрессии Двусторонний t-тест Помимо определения доверительных интервалов для коэффициентов, при построении регрессионных моделей важным является вопрос о проверке гипотез относительно некоторых конкретных значений отдельных коэффициентов регрессии. Такой вопрос возникает, например, если необходимо проверить, статистически значимо ли влияние регрессора (независимой переменной) на регрессанд (зависимую переменную). В этом случае можно сформулировать и попытаться проверить две гипотезы: нулевая гипотеза альтернативная гипотеза В общем случае, если на основе
анализа объекта моделирования можно
заранее (то есть еще до проведения
наблюдений) предположить (высказать
гипотезу), что регрессионный
коэффициент равен некоторому
значению
Тесты для проверки гипотез строятся на основе t-статистики вида
Правило принятия решений на основе статистики статистики (2.48) следующее: гипотеза H0 отклоняется, если
(эквивалентная запись этого
условия гипотеза H0 принимается, если
(эквивалентная запись Область значений t-статистики,
задаваемая выражением (2.49) называется областью
отклонения гипотезы H0, а
область (2.50)
- областью принятия гипотезы H0,
при уровне значимости Ошибки I и II рода. При проверке и принятии
гипотез существует риск допущения ошибок I и II рода.
Ошибка I рода возникает, если нулевая
гипотеза истинна, но она отвергается.
Ошибка II рода возникает, когда нулевая
гипотеза ложна, но она не отвергается.
Поскольку t - статистика - величина
случайная, то она может случайно принять
значение из области отклонения
нулевой гипотезы, даже если эта
гипотеза верна. Так как вероятность
попадания t-статистики в область
принятия гипотезы равна Интерпретация результатов тестирования. Если t-тест показывает, что на
уровне значимости Односторонний t-тест С помощью одностороннего t-теста
проверяют предположение (гипотезу) о
том, больше или нет коэффициент
нулевая гипотеза альтернативная гипотеза или Односторонний t-тест строится также, как двусторонний, однако область принятия решения, естественно, будет отличаться. Области принятия и отклонения для первой пары гипотез: область принятия гипотезы H0 область отклонения гипотезы H0 Области принятия и отклонения для второй пары гипотез: область принятия гипотезы H0 область отклонения гипотезы H0 Интерпретация результатов тестирования Если значения t-статистики
попадают в область принятия нулевой
гипотезы при заданном уровне
значимости Порядок проведения t-теста. 1. Сформулировать пару гипотез. 2. Определить табличное значение t-критерия для заданного уровня значимости. 3. Вычислить значение соответствующей t - статистики. 4. Сравнить величину t - статистики с табличным значением t - критерия. 5. Сделать вывод относительно возможности принятия гипотезы. Замечание. Нетрудно заметить, что
двусторонний t - тест для пары
гипотез Отметим, что аналогичные
тесты строятся и для проверки гипотез
относительно коэффициента 2.4.5. Проверка значимости коэффициента детерминации: F - тест В разделе 2.3.4. мы ввели понятие коэффициента детерминации R2 как показателя адекватности линейной регрессионной модели (меры степени линейной связи между переменными). Чем выше значение этого показателя, тем более точно линейная регрессия соответствует наблюдаемым данным. Но этот коэффициент определяется по выборочным данным и является в силу этого случайной величиной. Поэтому, даже если линейная связь между переменными y и x в парной линейной регрессии отсутствует (объясненная часть общей вариации зависимой переменной равна нулю), коэффициент детерминации может случайно принять большое значение, либо наоборот, при наличии линейной связи коэффициент детерминации может случайно принять значение, близкое к нулю. Таким образом, возникает вопрос: можно ли построить статистическую процедуру для проверки значимости коэффициента детерминации, подобно тому, как строились процедуры (тесты) для проверки гипотез о коэффициентах регрессии. Оказывается, что такую процедуру можно построить в рамках классической нормальной линейной модели регрессии, и она основана на использовании так называемой F-статистики, которая определяется следующим образом:
где ESS - объясненная сумма квадратов, RSS - остаточная сумма квадратов, p - число независимых переменных. Выражение (2.51) можно преобразовать и записать с использованием коэффициента детерминации
где TSS - полная сумма квадратов отклонений зависимой переменной. Заметим, что значения F - статистики не могут быть отрицательными. На основе F - статистики проверяется пара гипотез: Процедура проверки состоит в следующем: 1. вычисляем коэффициент детерминации; 2. вычисляем значение F - критерия (статистики) по формуле (2.52); 3.
находим табличное (критическое)
значение 4. если Очевидно, результаты F -
теста и t - теста для проверки
значимости коэффициента Пример 2.9. Проверка значимости коэффициента детерминации. Проверим гипотезу о
значимости коэффициента детерминации
в примере 2.1. Значение F-статистики,
вычисленное по формуле (2.52), равно: F=3701,286.
Критическое (табличное) значение F
- статистики для уровня значимости 0,05
равно Задание. Проверьте с помощью F - теста значимость коэффициентов детерминации для регрессий примера 1.2.
|
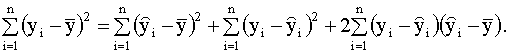
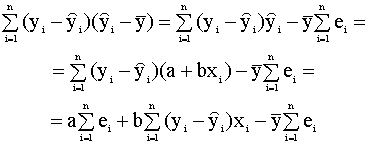
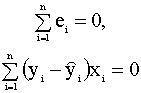
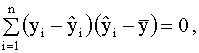
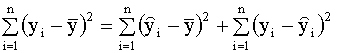
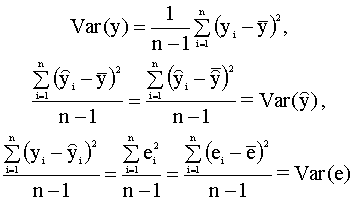
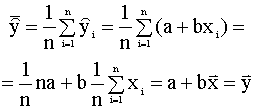
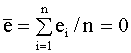 (здесь
использовано свойство (
(здесь
использовано свойство (