Эконометрика

2.5. Метод максимального правдоподобия (МП) для оценки параметров регрессии

Ранее мы упоминали, что кроме критерия наименьших квадратов, существуют и другие критерии, которые используются при оценивании параметров регрессии. Одним из таких, наиболее популярных критериев, является критерий максимума правдоподобия. Его применение возможно в условиях предположений нормальной линейной регрессии.

Идея метода максимального правдоподобия заключается в следующем. Составляется функция правдоподобия, которая равна совместной плотности вероятности наблюдений зависимой переменной при фиксированных значениях (реализации) независимой переменной .

Эта функция зависит от теоретических значений параметров модели, которые неизвестны. Однако можно определить их оценки, максимизируя функцию правдоподобия по этим параметрам. Тем самым мы определим параметры плотности, при которых вероятность получения выборки наблюдений y₁, y₂,...,y_n при заданных значениях наблюдений независимой переменной x₁, x₂,...,x_n, будет максимальна, то есть наиболее правдоподобные значения параметров (отсюда и название - функция правдоподобия). При выполнении условий Гаусса - Маркова совместная функция плотности вероятностей равна произведению плотностей отдельных наблюдений (это верно, поскольку случайные переменные u, согласно третьему условию Гаусса-Маркова, независимы в разных наблюдениях). Далее, поскольку случайная переменная u подчиняется нормальному распределению, то и будет плотностью нормального распределения. С учетом этого, функцию правдоподобия можно представить в виде

(2.53)

Так как логарифм функции правдоподобия lnL достигает максимума при тех же значениях искомых параметров, что и сама функция L, то удобнее максимизировать функцию

(2.54)

Необходимые условия максимума функции правдоподобия lnL имеют вид

	(2.55)
	(2.56)
	(2.57)

Уравнения (2.55), (2.56) по существу совпадают с необходимыми условиями минимума (2.9), (2.10) критерия наименьших квадратов. Их решение дает следующие оценки максимального правдоподобия коэффициентов и :

которые совпадают с оценками наименьших квадратов a и b (2.13), (2.14). Из уравнения (2.57) получаем оценку максимального правдоподобия дисперсии :

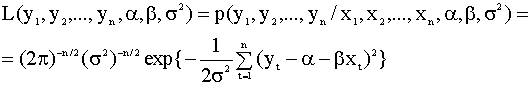
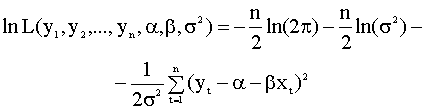
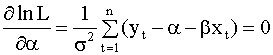
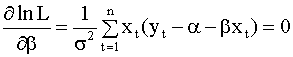
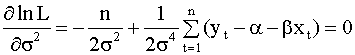
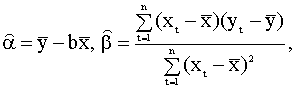
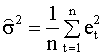
Эта оценка отличается от несмещенной оценки наименьших квадратов 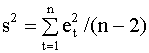и, следовательно, является смещенной. При больших n обе оценки дают близкий результат и при неограниченном возрастании n сходятся к истинному значению дисперсии, то есть оценка максимума правдоподобия, так же как и оценка наименьших квадратов, является состоятельной.