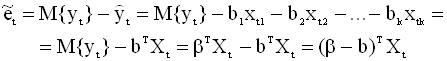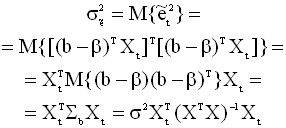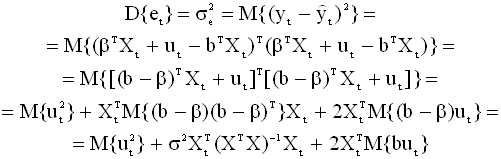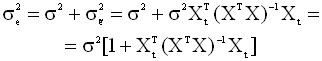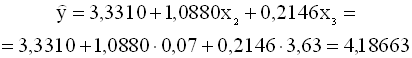Эконометрика

Глава 3 МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ

3.5. Точечное и интервальное прогнозирование на основе модели множественной регрессии

Основная цель построения регрессионной модели - получение значений зависимой переменной при некоторых заданных значениях независимых переменных, в общем случае не совпадающих с выборочными их значениями, использованными для оценки коэффициентов модели, но принадлежащих той же генеральной совокупности данных. В этом случае говорят о прогнозе регрессанда (зависимой переменной). Следует отличать прогноз математического ожидания регрессанда

и прогноз индивидуального значения регрессанда

как оценку реализации случайной переменной Y, здесь индекс t указывает на значение соответствующей переменной, в общем случае не совпадающее с наблюдаемым. Оба прогноза строятся в соответствии с уравнением

(3.61)

или

(3.62)

где вектор - столбец X_t=(x_t1,x_t2,...,x_tk)^T состоит из значений регрессоров, в общем случае не совпадающих с наблюдаемыми, то есть они лежат за пределами наблюдаемой выборки. Конкретные значения регрессоров задаются исследователем - эконометристом в соответствии с поставленной целью исследований. Уравнения (3.61), (3.62) определяют точечные прогнозы указанных величин. Качество этих прогнозов характеризуется дисперсиями ошибок прогнозов и шириной доверительных интервалов. И хотя прогнозы математического ожидания и индивидуального значения регрессанда совпадают (формально они определяются по одинаковым формулам), дисперсии ошибок и доверительные интервалы прогнозов будут различны.

Прогноз математического ожидания регрессанда: дисперсия ошибки прогноза и доверительный интервал (интервальный прогноз)

Ошибка точечного прогноза математического ожидания

(3.63)

В уравнении (3.63) единственной случайной величиной является вектор оценок b. Ошибка прогноза в классической линейной регрессии является линейной функцией оценок. Следовательно, статистические свойства ошибки определяются статистическими свойствами оценок параметров регрессии. Получим выражение для истинной (теоретической) дисперсии ошибки прогноза. Вспоминая определение дисперсии, учитывая формулу (3.27) для истинной ковариационной матрицы вектора оценок, а также то, что в силу свойства несмещенности оценок коэффициентов математическое ожидание ошибки , будем иметь

(3.64)

Полученная формула определяет теоретическое значение дисперсии. Оцененное значение дисперсии ошибки прогноза получится, если в формуле (3.64) теоретическое значение дисперсии случайной составляющей модели заменить его оценкой по формуле (3.42). Тогда получим, что оцененное значение дисперсии будет равно

(3.65)

и среднеквадратичное отклонение

(3.66)

Доверительный интервал прогноза математического ожидания регрессанда (интервальный прогноз) определяется следующим образом:

нижняя граница

(3.67)

верхняя граница

(3.68)

где определяется уравнением (3.61) или, что то же самое, (3.62); - табличное значение t - статистики для заданного уровня значимости и данного числа степеней свободы p=(n-k) и вычисляется по формуле (3.66).

Если оценки и интерпретировать как случайные величины, то можно сказать, что доверительный интервал со случайными границами (3.67), (3.68) с вероятностью накрывает истинное значение математического ожидания M{y_t} .

При определении доверительного интервала на основе конкретной выборки он может либо включать (примерно в 95 случаев из ста, если =0,05), либо не включать (примерно в 5 случаях из ста) истинное значение M{y_t}.

Замечание.

Нетрудно видеть, что , откуда следует несмещенность прогноза и равенство: .

Прогноз индивидуального значения регрессанда: дисперсия ошибки прогноза и доверительный интервал (интервальный прогноз)

Ошибка прогноза индивидуального значения регрессанда равна

(3.69)

Дисперсия ошибки

Случайная переменная y_t в классической модели линейной регрессии имеет дисперсию , равную дисперсии случайной составляющей модели u_t. Дисперсия оценки равна дисперсии ошибки и определяется по формуле (3.64). Поскольку случайные переменные u_t и b не коррелированы между собой (так как u_t некоррелирована с переменными y_i , i=1,2,…,n, входящими в выборку), то дисперсия ошибки e_t будет равна сумме дисперсий переменных y_t и . Таким образом, теоретическая дисперсия ошибки прогноза индивидуального значения зависимой переменной равна

(3.70)

Заметим, что дисперсия ошибки прогноза индивидуального значения регрессанда всегда больше (при прочих равных условиях) дисперсии ошибки прогноза его математического ожидания.

Эмпирические оценки дисперсии и среднеквадратического отклонения получатся, если в выражении (3.70) теоретическое значение дисперсии заменить ее несмещенной оценкой (3.42). Тогда оценка дисперсии будет равна

(3.71)

оценка среднеквадратического отклонения

(3.72)

Границы доверительного интервала для прогноза (интервальный прогноз) можно определить по формулам:

нижняя граница

верхняя граница

Очевидно, что поскольку среднеквадратичное отклонение , то (при прочих равных условиях), прогнозный интервал индивидуального значения регрессанда всегда будет больше прогнозного интервала для математического ожидания регрессанда.

Пример 3.7. (продолжение примера 3.1.).

Определим прогноз доходности компании A при условии, что доходности компаний B и C примут значения x₂=0,07 , x₃=3,63, и построим доверительные интервалы для прогноза среднего и индивидуального значений доходности компании A. Подставляя значения регрессандов в уравнение регрессии, получим

Среднеквадратичное значение прогноза среднего вычисляется по формуле (3.66) и равно . Табличное значение t - критерия при уровне значимости 0,05 и p=9 степенях свободы равно 2,179. Границы доверительного интервала ; . Среднеквадратичная ошибка прогноза индивидуального значения регрессанда вычисляется по формуле (3.72) и равна . Доверительный интервал для прогноза индивидуального значения имеет границы: (3,142;5,231). Естественно, этот интервал шире, чем доверительный интервал для прогноза среднего - прогноз индивидуальных значений менее надежен.

Задание. Выполните прогноз среднего и индивидуального значений зависимой переменной для модели примера 3.2. и постройте соответствующие доверительные интервалы.

Свойства точечных и интервальных прогнозов

Прогнозные оценки вида (3.62), полученные в данном разделе, являются наилучшими несмещенными линейными оценками, то есть для них справедлива теорема Гаусса-Маркова.