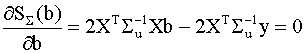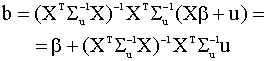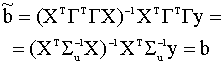Эконометрика

Глава 4. ОБОБЩЕНИЯ МОДЕЛИ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

4.2. Обобщенная регрессионная модель. Обобщенный метод наименьших квадратов

Рассмотрим обобщенную модель линейной регрессии с матрицей ковариаций вектора возмущений общего вида (4.1). Таким образом, мы отказываемся от предпосылки о гомоскедастичности и некоррелированности возмущений. Остальные предпосылки классической модели остаются в силе. Для оценивания параметров обобщенной модели можно использовать обобщенный метод наименьших квадратов. В предположении, что матрица ковариаций возмущений известна и не вырождена (заметим, что это предположение является по существу, дополнительной предпосылкой обобщенной модели), этот критерий имеет вид

(4.6)

Если матрица - диагональная (этот случай соответствует гетероскедастичным некоррелированным возмущениям), то оценки определяются из условия минимума суммы взвешенных квадратов ошибок (такой критерий иногда еще называют взвешенным критерием наименьших квадратов). Раскрывая скобки в (4.6), получим

Минимум целевой функции достигается в точке b, удовлетворяющей следующей системе линейных уравнений, записанной в векторно-матричной форме:

которую перепишем так

(4.7)

При выполнении предпосылок относительно матрицы регрессоров X - она должна иметь полный ранг, решение уравнения (4.7) можно записать в виде

(4.8)

Таким образом, оценка коэффициентов по обобщенному методу наименьших квадратов определяется формулой (4.8). Эта оценка является несмещенной. Действительно,

(4.9)

Применяя к обеим частям выражения (4.9) оператор математического ожидания, с учетом предпосылок модели, будем иметь

Используя выражение (4.9), нетрудно получить формулу для ковариационной матрицы вектора оценок коэффициентов обобщенной модели

(4.10)

Замечание.

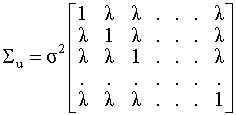
Для того, чтобы обобщенный МНК можно было использовать на практике, очевидно, необходимо знать матрицу ковариаций вектора возмущений модели. При применении обобщенного МНК в формулах (4.8), (4.9) вместо матрицы используют ее оценку. В общем случае эта матрица имеет n(n-1)/2 различных элементов, которые необходимо каким - либо образом оценить по имеющейся выборке наблюдений. Возможные подходы к решению данной задачи будут рассмотрены в последующих разделах.

Частный случай: постоянная пространственная корреляция возмущений

На практике возможна ситуация, когда возмущения модели удовлетворяют условию гомоскедастичности, но при этом существует одинаковая степень статистической взаимосвязи между случайными составляющими в разных наблюдениях. Это может иметь место, если анализируются однородные группы элементов в пространственной выборке. В этом случае матрица ковариаций вектора возмущений имеет следующую структуру:

Ковариации одинаковы для всех . При такой форме матрицы ковариаций оценки, полученные с использованием обычного метода наименьших квадратов, обладают такими же статистическими свойствами как и в классической линейной модели. Оценивание модели с постоянными ковариациями существенно проще, так как для нее по сравнению с классической моделью достаточно оценить только один дополнительный параметр .

Статистические свойства оценок обобщенного метода наименьших квадратов

Выше мы установили, что использование обычного МНК для оценивания обобщенной модели не позволяет получить оценки, обладающие такими же статистическими свойствами, как и оценки классической модели - теорема Гаусса-Маркова для них не выполняется. В частности, такие оценки не будут эффективными. Однако оценки обобщенного МНК такими свойствами обладают.

Теорема Айткена (Эйткена). Линейная оценка вида

вектора коэффициентов обобщенной линейной модели регрессии имеет наименьшую матрицу ковариаций в классе линейных несмещенных оценок (то есть, является наилучшей в смысле минимума дисперсий оценок коэффициентов).

Доказательство. Ранее мы установили, что обобщенная оценка (4.8) является несмещенной. Покажем, что она является также оптимальной (наилучшей, эффективной) в смысле минимума дисперсий оценок коэффициентов. Поскольку матрица симметричная положительно определенная, то и обратная матрица будет симметричной положительно определенной. Из матричного анализа известно, что любую симметричную положительно определенную матрицу можно представить в виде

где Г - некоторая невырожденная матрица. Умножим обе части уравнения обобщенной линейной регрессии

(4.11)

слева на матрицу Г. Получим

Обозначим и запишем

(4.12)

Таким образом, уравнение (4.12) получается в результате невырожденного преобразования уравнения (4.11) обобщенной линейной регрессии. Покажем, что оно удовлетворяет предпосылкам классической линейной модели. Действительно, , .

Следовательно, обычная МНК-оценка параметров модели (4.12) вида

(4.13)

удовлетворяет условиям теоремы Гаусса-Маркова и является наилучшей (оптимальной) линейной несмещенной оценкой вектора . Но нетрудно видеть, что

и, следовательно, обобщенная оценка также является наилучшей в классе линейных, что и требовалось доказать.

Замечание.

При анализе адекватности классической модели регрессии мы в качестве характеристики качества модели использовали коэффициент детерминации или скорректированный коэффициент детерминации. К сожалению, для обобщенной регрессионной модели коэффициент детерминации не может служить надежным показателем качества.