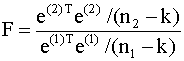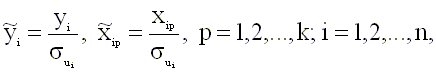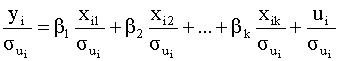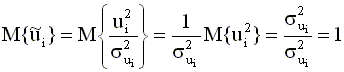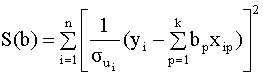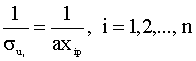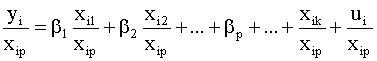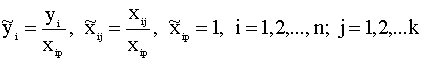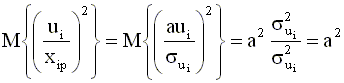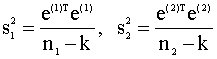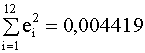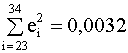|
4.3. Обобщенная линейная модель с гетероскедастичными возмущениями В этом разделе мы рассмотрим
частный случай обобщенной модели
регрессии, часто встречающийся на
практике, а именно, предположим, что
дисперсия случайного члена модели
зависит от номера наблюдения. Это
означает, что хотя бы для одного
значения i (i=1,2,…,n)
Естественно, что прежде чем строить модель с гетеросткедастичными возмущениями, необходимо убедиться, что реальные данные соответствуют этому случаю. Для этого разработаны различные методы диагностики (проверки) данных на гетероскедастичность, основанные на статистических тестах. Если же проведенное тестирование подтверждает гипотезу гетероскедастичности, то возможны два способа оценки (построения) модели: 1) попытаться избавиться от гетероскедастичности путем преобразования модели (провести коррекцию гетероскедастичности) и затем использовать обычный МНК; 2) использовать обобщенный метод наименьших квадратов. Первый способ, вообще говоря, предпочтительнее, так как он часто не требует оценивания всех n дисперсий случайной составляющей. Диагностика гетероскедастичности: тест Гольдфельда-Квандта Рассмотрим наиболее простой, наглядный и часто используемый тест на гетероскедастичность - тест Гольдфельда-Квандта. Тест на гетероскедастичность состоит в проверке следующей пары гипотез: Возможны два варианта проведения теста. Первый вариант 1). Все n наблюдений делят
на две группы. В первую группу
включают наблюдения с
предположительно меньшей дисперсией,
обозначим их количество n1,
ко второй группе относят оставшиеся n2
= n - n1 наблюдений. Тем самым
вектор (вектор-столбец) наблюдений
зависимой переменной разбивается на
два подвектора, 2). Для каждой из групп наблюдений строят независимые регрессии с использованием обычного МНК. Таким образом, оценивают две модели
3). Формируют статистику
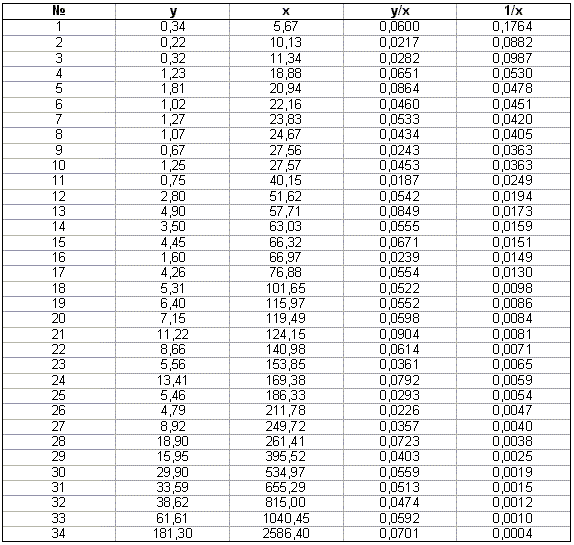
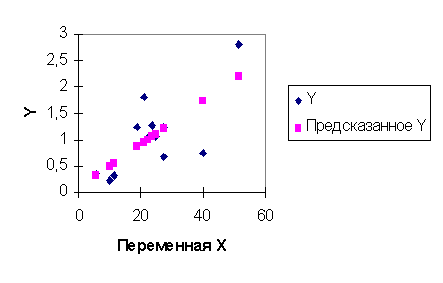
где e(1), e(2) - векторы остатков моделей (4.14), (4.15). Статистика (4.16) имеет F - распределение Фишера с (n2 - k, n1 - k) степенями свободы (при выполнении предпосылки о нормальном распределении случайного члена). 4). Проверяют гипотезу H0, которая отклоняется, если Замечание. Данную процедуру тестирования, очевидно, можно применять, только если выполнены предпосылки классической модели регрессии, за исключением гомоскедастичности. Второй вариант Если число наблюдений достаточно велико, то можно применить второй вариант теста. Он отличается от первого тем, что при разделении наблюдений на группы исключают m средних наблюдений. Таким образом, в первую группу включают первые из упорядоченных по убыванию дисперсий n1 наблюдений, а во вторую - последние n2 = (n - n1 - m) наблюдений. Такой прием увеличивает чувствительность теста Гольдфельда - Квандта (увеличивается мощность теста). В этом случае при справедливости гипотезы о гетероскедастичности (альтернативной) и при удачном разбиении наблюдений на группы числитель в выражении (4.16) будет существенно больше знаменателя. К сожалению, не существует формально обоснованных рекомендаций о том, в каких пропорциях формировать группы наблюдений и сколько наблюдений исключать. На основе опыта использования теста Гольдфред и Квандт рекомендуют при n=30 исключать восемь наблюдений (m=8), при n=60 - шестнадцать (m=16). При этом не следует забывать, что число наблюдений в двух регрессиях (4.14), (4.15) должно быть, по крайней мере, не меньше, чем количество оцениваемых коэффициентов регрессии. Пример 4.1. В таблице 4.1. приведены числовые данные о государственных расходах на образование (y) и валовом внутреннем продукте (x) для 34 стран (источник: К. Доугерти, 1997, с. 205, [16]). Проверим эти данные на наличие гетероскедастичности, используя критерий Гольдфельда - Квандта. Данные таблицы 4.1. упорядочены по возрастанию переменной x. Применение обычного метода наименьших квадратов позволяет получить следующую регрессионную зависимость расходов на образование от валового внутреннего продукта
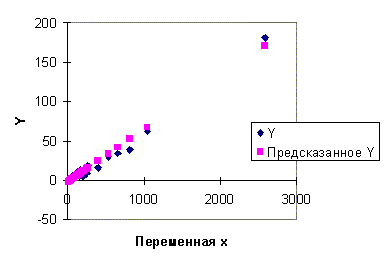
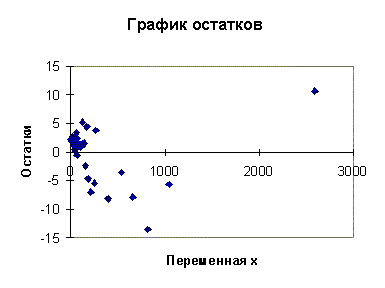
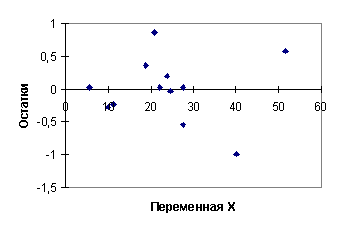
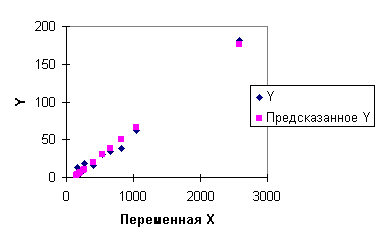
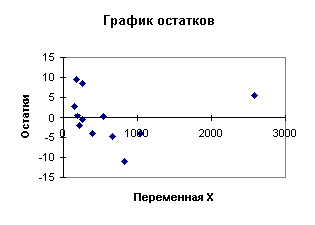
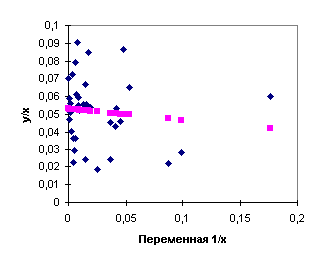
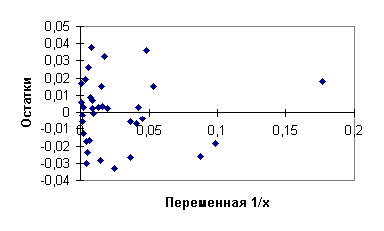
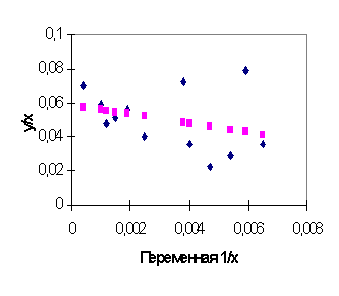
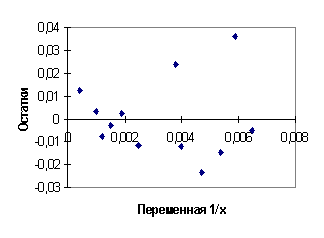
На рис. 4.1. зависимость (4.17) изображена графически. На рис. 4.2. показана диаграмма рассеяния для остатков регрессионной модели (4.17). Из анализа этой диаграммы можно предположить, что дисперсия остатков возрастает с ростом переменной x. С целью применения теста Гольдфельда - Квандта построим две "частные" регрессии. Для этого возьмем данные по первым n1 = 12 и последним n2 = 12 странам. Таким образом, из выборки мы исключаем 10 средних наблюдений. Регрессионная зависимость, построенная с помощью МНК по первым 12 наблюдениям (первая "частная" регрессия), имеет вид
Регрессионная зависимость, построенная по последним 12 наблюдениям (вторая "частная" регрессия) имеет вид
На рис. 4.4, 4.5 изображены соответственно графики первой частной регрессии (4.18) и ее остатков, на рис. 4.5, 4.6 представлены аналогичные зависимости для второй частной регрессии (4.19). Интересно сравнить качество построенных регрессионных моделей по коэффициенту детерминации. Для модели (4.17), построенной по всему набору данных, R2 = 0,9794. Для модели (4.18), построенной по первым 12 наблюдениям, R2 = 0,5309. Для модели (4.19), построенной по последним 12 наблюдениям, R2 = 0,9854. Сравнивая коэффициенты детерминации, видим, что первая "частная" регрессия (4.18) значительно хуже аппроксимирует наблюдаемые данные, чем вторая (4.19). В тоже время и модель (4.17), построенная по всем наблюдениям, имеет коэффициент детерминации несколько меньше, чем вторая "частная" модель. Таким образом, если бы в нашем распоряжении были данные наблюдений только по первым 12 странам, наш вывод о существовании линейной зависимости был бы пессимистичным. Если бы мы имели данные только по последним 12 странам, наш вывод о линейной зависимости был бы излишне оптимистичным. Отсюда можно сделать поучительный вывод: при ограниченном числе наблюдений заключение относительно качества модели не может быть окончательным. Нельзя ожидать, что добавление новых наблюдений улучшит модель с точки зрения показателей адекватности. Но добавление наблюдений позволяет углубить представление о реальной зависимости между переменными. Задание. Определите эмпирические дисперсии оценок коэффициентов всех моделей данного примера и постройте для них доверительные интервалы. Сделайте дальнейшие выводы относительно качества моделей и влияния дополнительных наблюдений. Продолжим анализ остатков. Сумма квадратов остатков первой частной регрессии равна e(1)Te(1) = 2,68, второй e(2)Te(2)=388,24. Значение F - статистики определяется из соотношения
поскольку n2 - k = n1
- k = 10. Оно равно F = 144,9. Табличное
значение F - статистики при уровне
доверия Поскольку Устранение гетероскедастичности: преобразование модели и метод взвешенных наименьших квадратов При наличии гетероскедастичности обычный метод наименьших квадратов дает состоятельные и несмещенные оценки неизвестных коэффициентов, но оценка матрицы ковариаций смещена и несостоятельна. Если матрица ковариаций вектора случайных возмущений имеет диагональный вид (отсутствует корреляция между различными наблюдениями) и ее диагональные элементы - дисперсии случайного члена в различных наблюдениях - известны, то в этом случае исходная модель преобразуется таким образом, что для ее оценки можно применить обычный метод наименьших квадратов и оценки будут иметь желательные свойства. Исходные данные преобразуются следующим образом:
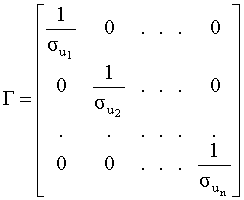
то есть каждое наблюдение регрессанда и каждый элемент i - ой строки матрицы регрессоров делится на соответствующее стандартное отклонение случайного члена. Данным преобразованиям соответствует следующая матрица преобразования:
Преобразованная модель имеет вид
причем преобразованная
случайная составляющая
Таким образом, преобразованная модель (4.20) получилась гомоскедастичной и для ее оценивания можно применить обычный МНК. Критерий МНК в этом случае имеет вид
где
Из выражения (4.22) видно, что проведенное преобразование приводит к модификации критерия метода наименьших квадратов, заключающейся в том, что теперь ошибки (остатки) модели в каждом наблюдении не просто складываются, а берутся с "весами", причем наблюдениям с меньшими дисперсиями (более точным) придаются большие веса. Это позволяет получать эффективные оценки, в отличие от обычного МНК. Поэтому обобщенный метод наименьших квадратов для рассматриваемой модели с гетероскедастичностью называют методом взвешенных наименьших квадратов. Определение матрицы преобразований Известно множество способов определения матрицы преобразований Г. Мы рассмотрим два таких способа, которые можно рекомендовать к применению на практике. 1).Определение
Г без статистической оценки.
Иногда на основе анализа имеющихся
статистических данных (наблюдений)
можно предположить, что стандартное
отклонение возмущений является
линейной однородной функцией одной из
независимых переменных, скажем, Если это действительно так, то тогда диагональные элементы матрицы преобразований Г определяются по формуле
Преобразование исходного
уравнения регрессии сводится к
делению левой и правой частей на
переменную xip
Переменные преобразованной модели определяются соотношениями
Заметим, что преобразованые переменные (4.24) не зависят от коэффициента пропорциональности "a", поскольку он входит в качестве множителя в правую и левую части преобразованного уравнения и попросту сокращается. Дисперсия случайного члена в преобразованной модели (4.23) будет постоянна для всех наблюдений. Действительно, имеем
Данный способ устранения
гетероскедастичности обосновывает
следующую практическую
рекомендацию: если
существует несколько равнозначных (эквивалентных)
с экономической точки зрения способов
представления переменных модели (например,
не имеет значения, используется в
модели в качестве регрессанда
переменная 2). Второй способ применяется,
если из анализа данных можно
предположить, что дисперсия
возмущений принимает только два
значения - гетероскедастичность между
гомоскедастичными группами.
Предположим, что в первых n1
наблюдениях возмущения имеют
одинаковые дисперсии
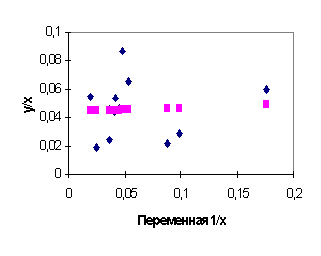
Диагональные элементы матрицы преобразований имеют вид: первые n1 элементов равны 1/s1, остальные - 1/s2 . Преобразование исходной модели сводится к делению первых n1 уравнений на s1 и остальных - на s2. Далее, оцениваем преобразованную регрессию с использованием обычного МНК. Описанную процедуру устранения гетероскедастичности можно обобщить на случай, когда дисперсия принимает не два, а несколько значений. Пример 4.2. Рассматривая пример 4.1. мы установили, что в регрессии, построенной по данным таблицы 4.1, остатки гетероскедастичны. Предположим, что стандартное отклонение возмущений модели является линейной однородной функцией независимой переменной и для устранения гетероскедастичности применим первый из описанных выше способов. Преобразование исходной модели сводится к делению правой и левой частей парной регрессии на значение регрессора xi. Таким образом, преобразованная модель имеет вид
где
Подчеркнем, что
преобразованная модель (4.25) объясняет
регрессионную зависимость переменной
y/x от независимой переменной 1/x
и от нее не следует ожидать хорошей
объясняющей способности, поскольку в
преобразованном уравнении
объясняющие свойства независимой
переменной 1/x зависят от
значимости коэффициента После обратного преобразования переменных модели (4.25) к исходным переменным, получаем регрессию Проверим, действительно ли нам удалось устранить гетероскедастичность. Для этого к преобразованной модели (4.25) применим тест Гольдфельдта - Квандта. Используя преобразованные данные таблицы 4.1, построим две "частные" регрессии: первую по первым 12 наблюдениям, вторую - по последним 12 наблюдениям и вычислим суммы квадратов остатков для этих двух регрессий. Применяя метод наименьших квадратов, получим первую регрессию
и вторую
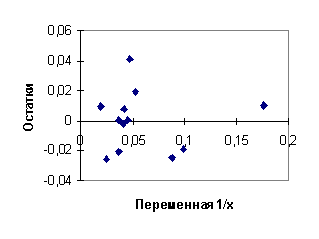
Диаграммы рассеяния, линии регрессии и графики остатков для регрессий (4.27), (4.28) приведены на рис. 4.9, 4.10, 4.11, 4.12. Суммы квадратов остатков для этих регрессий:
Значение F - статистики
равно F=0,7287. Критическое значение
|
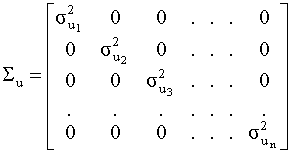
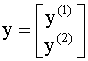 ,
размерностей n1 и n2,
а матрица наблюдений независимых
переменных - на две подматрицы,
,
размерностей n1 и n2,
а матрица наблюдений независимых
переменных - на две подматрицы,  , размерностей (n1 x k) и (n2
x k) соответственно.
, размерностей (n1 x k) и (n2
x k) соответственно.