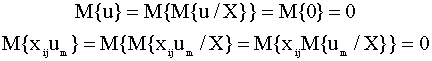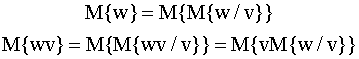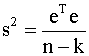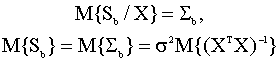Эконометрика

Глава 4. ОБОБЩЕНИЯ МОДЕЛИ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

4.6. Линейные модели регрессии со стохастическими регрессорами

Одной из основных предпосылок классической линейной регрессии была предпосылка о том, что независимые переменные - регрессоры являются детерминированными величинами. Эта предпосылка имеет существенное значение для установления ряда желательных свойств МНК - оценок регрессии - несмещенности, эффективности, состоятельности. Однако на практике эта предпосылка, к сожалению, часто не выполняется, и, следовательно, классическая модель становится неадекватной наблюдаемым данным (подробное обсуждение значения этой предпосылки при построении линейной регрессии и последствия, к которым приводит ее не выполнение см. п. 4.1.1).

В данном разделе рассмотрим модель со стохастическими регрессорами, которая при определенных предположениях обладает свойствами, подобными свойствам классической модели.

Итак, рассмотрим линейную модель

(4.48)

где, как и ранее, y - вектор - столбец зависимых переменных, X - матрица наблюдений независимых переменных, u - вектор - столбец случайных составляющих модели. Принципиальным отличием регрессии (4.48) от рассматриваемых ранее моделей является то, что теперь матрица независимых переменных (регрессоров) предполагается не детерминированной, а случайной (случайная матрица - это матрица, у которой хотя бы один элемент является случайной величиной). Для простоты мы не делаем различий между обозначениями случайных величин регрессии (4.48) и их выборочных значений.

Предположим, что для данной модели выполнены следующие предпосылки.

1) Условное математическое ожидание случайной составляющей

2) Условная ковариационная матрица случайной составляющей

Данная предпосылка означает, что условные дисперсии компонент вектора u - постоянные величины - модель условно гомоскедастична.

3) При всех реализациях матрица X имеет полный ранг.

Замечание.

При формулировке данных предпосылок мы использовали понятие условного математического ожидания случайной величины. В модели со стохастическими регрессорами в общем случае предполагается, что регрессоры и случайный член модели статистически зависимы. Условное математическое ожидание случайной величины u вычисляется при условии, что случайная матрица X приняла некоторое определенное значение, то есть при некоторой фиксированной реализации случайной матрицы регрессоров X. Если случайные величины u и X независимы, то случайная величина u принимает то или иное значение независимо от того, какое значение принимает случайная величина X и, следовательно, условное математическое ожидание и .

Покажем, что из первой предпосылки модели следует некоррелированность вектора u и матрицы регрессоров X, то есть для всех i=1,2,…,n, j=1,2,…,k, m=1,2,…,n. (Напомним, что некоррелированность случайных величин не означает их независимость. Эти понятия эквивалентны только в случае нормально распределенных случайных величин). Действительно,

Здесь мы использовали следующие свойства условных математических ожиданий: для зависимых случайных величин w, v,

Выражения для МНК - оценки вектора коэффициентов, ковариационной матрицы вектора оценок и ее оценки, дисперсии возмущений и ее оценки в модели (4.48) со стохастическими регрессорами для конкретной реализации матрицы регрессоров X формально имеют такой же вид, как для модели с детерминированными регрессорами (разумеется, при условии выполнения предпосылок модели):

(4.49)

(4.50)

(4.51)

(4.52)

однако теперь их следует понимать как оценки соответствующих условных (при заданной реализации случайной матрицы X) величин.

Можно показать, что:

1) оценка (4.49) является условно и безусловно несмещенной оценкой вектора коэффициентов, то есть

2) оценка (4.52) дисперсии возмущений является условно и безусловно несмещенной, то есть

3) оценка (4.51) ковариационной матрицы вектора оценок является условно и безусловно несмещенной, то есть

Задание.

Докажите свойства 1).- 3)., используя правила преобразования условных математических ожиданий.

Таким образом, при выполнении условий 1) - 3) Гаусса - Маркова в модели со стохастическими регрессорами МНК - оценки являются несмещенными. Для таких моделей имеет место условный вариант теоремы Гаусса-Маркова.

Условный вариант теоремы Гаусса-Маркова.

среди всех линейных условно несмещенных оценок вектора коэффициентов его МНК - оценка вида (4.49) имеет наименьшую условную ковариационную матрицу (дисперсии оценок отдельных коэффициентов минимальны).

Задание.

Докажите условный вариант теоремы Гаусса - Маркова.

Таким образом, при выполнении условий Гаусса - Маркова, МНК - оценки в модели со стохастическими регрессорами имеют свойства (относительно условных математических ожиданий), аналогичные свойствам классической модели. Однако если случайные величины X и u коррелированы, то в общем случае МНК - оценки будут смещенными и несостоятельными.