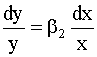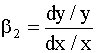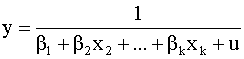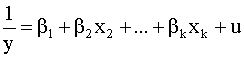Эконометрика

Глава 4. ОБОБЩЕНИЯ МОДЕЛИ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

4.9. Нелинейные модели регрессии: методы линеаризации

До сих пор мы рассматривали линейные регрессионные модели и их обобщения, которые так же были линейными моделями. Для таких моделей получены уравнения для оценок параметров и их характеристик, доказаны свойства оценок, разработаны процедуры тестирования и проверки адекватности. Уравнения, описывающие эти модели и соответствующие процедуры, имеют наиболее простой вид и достаточно просто реализуются на практике в виде вычислительных алгоритмов. Поэтому исследователю можно дать следующую рекомендацию: если есть возможность построить линейную модель с большим количеством регрессоров, вместо нелинейной модели, пусть даже и с меньшим числом регрессоров, то лучше предпочесть линейную модель.

К сожалению, при моделировании реальных социально-экономических процессов далеко не всегда можно описать процесс с помощью линейной зависимости. Однако, можно попытаться так преобразовать нелинейную модель, чтобы свести ее к линейной. Мы покажем, что во многих случаях это удается сделать, и достаточно простым способом.

Нелинейная регрессия, линейная относительно параметров

Широкий класс нелинейных моделей регрессии можно представить в виде

(4.61)

где - известные, в общем случае нелинейные, функции наблюдаемых независимых переменных, (j=1,2,…,k; i=1,2,…,n) (напомним, что переменные все равны единице).

Нетрудно заметить, что нелинейная модель вида (4.61) легко сводится к линейной, если произвести следующее преобразование переменных: , то есть в уравнении (4.61) в качестве регрессоров рассматривать функции независимых (объясняющих) переменных, значения которых можно вычислить, имея наблюдения независимых переменных.

Таким образом, если регрессионная модель нелинейна относительно независимых переменных, но линейна относительно коэффициентов регрессии и случайной составляющей, то ее можно рассматривать как линейную, если в качестве регрессоров взять преобразованные независимые переменные.

Регрессия, нелинейная относительно параметров и случайного члена

Многие экономические процессы можно описать нелинейными функциями вида

(4.62)

Правая часть уравнения (4.62) представляет собой нелинейную функцию как относительно параметров (степенную), так и случайной составляющей. В этом случае говорят, что модель содержит мультипликативные возмущения. В качестве примера подобного вида зависимостей можно привести хорошо известную производственную функцию Кобба - Дугласа (ее эконометрическую версию). Несмотря на кажущуюся сложность нелинейной зависимости (4.62), ее также можно свести к линейной путем логарифмического преобразования. Действительно, логарифмируя правую и левую части уравнения (4.62), получим

(4.63)

Уравнение (4.63) линейно относительно логарифмов переменных модели. Таким образом, вводя преобразования переменных вида нелинейную модель (4.62) можно свести к линейной.

Интерпретация коэффициентов логарифмической регрессии

Рассмотрим модель с одним регрессором

(4.64)

Продифференцируем правую и левую части этого уравнения, получим

откуда

(4.65)

Правая часть формулы (4.65) определяет эластичность переменной y по x. Понятие эластичности широко используется в экономическом анализе. Коэффициент эластичности показывает, на сколько процентов изменится величина переменной y при изменении переменной x на один процент. Таким образом, в модели (4.64) параметр - это ни что иное, как коэффициент эластичности переменной y по x.

Обобщая, можно сказать, что в многомерной логарифмической модели (4.63) коэффициенты , (j=2,3,…,k) - это эластичности зависимой переменной y по переменным .

Важные замечания

1) Следует помнить, что логарифмическое преобразование можно применять только в случае, если переменные исходной нелинейной модели принимают положительные значения. В противном случае (при отрицательных значениях переменных) логарифмическая функция не определена.

2) Если в исходной модели возмущения нормально распределены, то преобразованные возмущения этим свойством обладать не будут, что приводит к проблемам с применением тестов, которые основаны на предположении о нормальном распределении возмущений.

3) При нелинейных преобразованиях, подобных логарифмическому, нельзя утверждать, что свойства оценок преобразованной модели после обратного преобразования сохранятся и для исходной модели (будут иметь место и для исходной модели). В частности, оценка вида параметра (здесь - оценка параметра в преобразованной модели) не будет обладать теми же свойствами, что и оценка .

4) Если случайный член в уравнение (4.62) входит аддитивно, то в этом случае модель невозможно преобразовать так, чтобы свести ее к линейной.

Некоторые типичные часто применяемые в эмпирических исследованиях нелинейные эконометрические модели

1) Полиномиальная:

2) Логарифмическая (линейная относительно логарифмов)

Заметим, что в данное уравнение, в отличие от (4.63), шумы входят аддитивно.

3) Экспоненциальная:

4) Обратная:

или

5) Правая полулогарифмическая:

6) Левая полулогарифмическая:

7) Интерактивная модель (модель взаимодействия):

Мы рассмотрели типичных представителей класса нелинейных функций, которые можно преобразовать к линейному виду. К сожалению, не для всех нелинейных зависимостей такие преобразования возможны. Примером нелинеаризуемой функции может служить модель вида:

Для оценивания подобных моделей можно использовать метод наименьших квадратов, однако в данном случае его применение приводит к необходимости решения системы нелинейных уравнений, которую, как правило, можно решить только численно, используя специальные численные методы. Здесь этот вопрос подробно не рассматривается, отметим только, что задача построения и изучения свойств нелинейной (и не сводящейся к линейной) регрессии существенно сложнее задачи построения линейной (или сводящейся к линейной) регрессии.