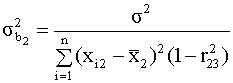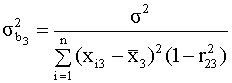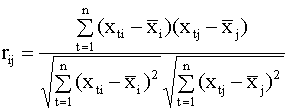Эконометрика

Глава 4. ОБОБЩЕНИЯ МОДЕЛИ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

4.8. Мультиколлинеарность: последствия, признаки и методы ее устранения

Одна из предпосылок линейной множественной регрессии - отсутствие коллинеарности (линейной зависимости) между регрессорами. Однако в эмпирических эконометрических исследованиях функциональная линейная зависимость встречается не часто, но возможно существование высокой корреляции между двумя или несколькими независимыми переменными. В этом случае говорят о проблеме мультиколлинеарности. Рассмотрим более подробно, к каким последствиям приводит коллиненарность регрессоров.

Увеличение дисперсий оценок коэффициентов

Эффект увеличения дисперсий проиллюстрируем на примере регрессии с двумя (не считая вспомогательного) регрессорами

(4.57)

Здесь y, u - скалярные случайные переменные. Формулы для истинных дисперсий МНК-оценок параметров и можно записать в виде:

(4.58)

(4.59)

где - коэффициент парной корреляции между и . Из формул (4.58) и (4.59) видно, что при увеличении абсолютной величины коэффициента корреляции , дисперсии оценок возрастают и, следовательно, их качество ухудшается. Выводы относительно истинных дисперсий оценок коэффициентов сохраняются и для выборочных оценок этих величин.

Задание.

Используя общую формулу для ковариационной матрицы оценок коэффициентов регрессии (3.27) получите формулы (4.58), (4.59).

Неидентифицируемость модели и неустойчивость оценок

Если существует функциональная линейная зависимость между регрессорами (столбцы матрицы X линейно зависимы), то говорят, что существует полная коллинеарность. В этом случае и дисперсии становятся равными бесконечности. Это соответствует случаю, когда матрица регрессоров X вырождена (не полного ранга), что в свою очередь приводит к вырожденности матрицы и невозможности вычисления обратной матрицы и, следовательно, оценок коэффициентов. Таким образом, нарушается предпосылка об идентифицируемости модели или, другими словами, регрессионная модель становится неидентифицируемой.

Для модели вида (4.57) функциональная зависимость между регрессорами означает, что можно выразить явную зависимость , где . С учетом этого, уравнение (4.57) можно записать в виде

(4.60)

Уравнение (4.60) определяет парную линейную регрессию, для которой можно оценить коэффициент , но не отдельно оценки коэффициентов и .

При сильной (но не функциональной) связи регрессоров (сильной коллинеарности) матрица становится плохо обусловленной - ее определитель близок к нулю. Это приводит к тому, что вычисленные по методу наименьших квадратов оценки будут неустойчивыми - малые изменения в исходных данных приводят к большим изменениям оценок, вплоть до смены их знака.

Увеличение доверительных интервалов

Оценки стандартных отклонений входят в формулы для доверительных интервалов коэффициентов (см. глава 3, п. 3.4.4): . Но поскольку с увеличением степени коллинеарности регрессоров возрастают дисперсии (и стандартные отклонения) оценок (и их оценки), то возрастают и доверительные интервалы. К аналогичным последствиям приводит коллинеарность и для доверительных интервалов прогноза регрессанда (его математического ожидания и индивидуальных значений).

Признаки (меры) коллинеарности регрессоров

Выше мы установили основные отрицательные последствия коллинеарности регрессоров. В эмпирических исследованиях редко проявляется полная коллинеарность, однако отрицательные последствия даже не полной коллинеарности могут быть весьма существенны. Естественно попытаться каким-то образом оценить степень коллинеарности регрессоров - ввести меру коллинеарности и по ней судить о степени отрицательного влияния этого эффекта. К сожалению, не возможно однозначно и наглядно определить уровень границы, которая отделяет существенную и несущественную коллинеарность. Рассмотрим некоторые из возможных мер коллинеарности.

Мерой коллинеарности может служить определитель матрицы то есть величина . Если он близок к нулю, то говорят, что матрица плохо обусловлена. Это является признаком того, что существует близкая к линейной зависимость между регрессорами. К сожалению, трудно сказать, при каком значении определителя можно считать коллинеарность не существенной, а начиная с какого ее следует считать существенной и, следовательно, искать способы устранения. Тем не менее, если определитель близок к нулю, то это является сигналом к тому, что можно ожидать неприятных эффектов при вычислении оценок.

Другой мерой коллинеарности может служить определитель корреляционной матрицы регрессоров. Корреляционная матрица регрессоров имеет вид

ее элементы - коэффициенты корреляции между i - ым и j - ым регрессорами. Очевидно, при формировании матрицы R нет необходимости учитывать вспомогательный регрессор . Оценки коэффициентов корреляции можно вычислить по формуле

Определитель матрицы R меняется в границах: . При полной коллинеарности (объясните, почему). Если коллинеарность отсутствует, то . Любое промежуточное значение указывает на существование коллинеарности, а при значении , близком к нулю, говорят о сильной (существенной) коллинеарности. К сожалению, этот показатель также не может служить однозначной мерой степени коллинеарности, он служит лишь индикатором возможного наличия сильной коллинеарности, но не указывает однозначно ее "источника" (конкретных регрессоров, из-за которых возникает этот эффект).

До сих пор мы рассматривали обобщенные (интегральные) показатели степени коллинеарности. Можно попытаться оценить степень коллинеарности регрессоров, анализируя отдельные элементы корреляционной матрицы. В модели регрессии с двумя регрессорами исчерпывающей мерой коллинеарности регрессоров служит коэффициент корреляции . При большем количестве регрессоров, если абсолютная величина хотя бы одного из коэффициентов корреляции близка к единице, то это сигнализирует о наличии сильной коллинеарности. Однако, эффект сильной коллинеарности может иметь место и без этого, то есть близость к единице коэффициентов корреляции (хотя бы одного) не является необходимым условием сильной коллинеарности. Тем не менее, анализ корреляционной матрицы регрессоров позволяет получить полезную информацию о возможном наличии коллинеарности и, в отдельных случаях, выявить причастные к этому регрессоры.

Рекомендации по устранению коллинеарности

Коллинеарность регрессоров может представлять серьезную проблему при построении моделей множественной регрессии. Поэтому важно, во-первых, убедиться, что модель свободна от существенной коллинеарности, и, во- вторых, обнаружить (не пропустить) существенную коллинеарность, если она имеет место.

Существуют различные подходы к устранению коллинеарности. В рамках данного курса можно рекомендовать следующее: изменить спецификацию модели, удалив из нее регрессор, который сильно коррелирует с другими. Однако, при этом следует иметь ввиду, что отбрасывание существенной независимой переменной, которая действительно воздействует на зависимую переменную, может привести к искажению модели и нарушению предпосылки о правильной спецификации (так называемым ошибкам спецификации), что, в свою очередь, приводит к другим неприятным последствиям (см. п. 4.1.4). Поэтому, при определении кандидатов на удаление, следует учитывать содержательный (экономический) смысл переменных и степень их влияния на зависимую переменную.