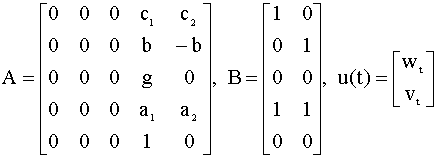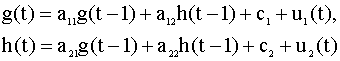Эконометрика

Глава 6. АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ

В данной главе рассматриваются современные методы анализа многомерных временных рядов, в том числе частично наблюдаемых и нелинейных. Вводятся фундаментальные понятия состояния и пространства состояний, на которых базируется современная теория многомерных систем. Рассматривается использование такого мощного инструмента анализа, как фильтр Калмана.

6.1. Модели многомерных временных рядов. Примеры процессов, описываемых моделями многомерных рядов. Понятие пространства состояний

До сих пор мы рассматривали одномерные временные ряды, то есть ряд представлял собой скалярную величину, наблюдаемую в последовательные моменты времени. Однако уже при рассмотрении моделей авторегрессии

(6.1)

оказывается, что состояние процесса в момент t зависит от его значений в несколько предыдущих моментов времени y_t-1, y_t-2,...,y_t-p, то есть, по существу, от вектора

размерности p (под вектором здесь, как и ранее, понимаем вектор-столбец). Скалярное разностное уравнение (6.1) порядка p можно записать в виде векторного уравнения первого порядка. Действительно, введем вектор , размерности p, и матрицу размера (p x p)

Тогда данное уравнение можно записать в векторном виде

(6.2)

Нетрудно заметить, что первое уравнение из (6.2), то есть уравнение для компоненты , совпадает с уравнением авторегрессии (6.1), а остальные представляют собой просто тождества.

Обобщая, рассмотрим векторное стохастическое разностное уравнение первого порядка ( векторный случайный процесс)

(6.3)

где - p - мерный вектор, компоненты которого зависят от времени; - случайный вектор (вектор, компоненты которого - случайные величины) размерности s с нулевым средним и ковариационной матрицей , причем , при ; A - квадратная матрица размера p с элементами (в теории линейных систем ее называют переходной матрицей); B - прямоугольная матрица размера p x s с элементами . С помощью моделей вида (6.3) описываются многие процессы (системы), в том числе в экономике.

Пример 6.1. Эконометрическая версия модели Самуэльсона -Хикса

Модель Самуэльсона - Хикса (ее эконометрический вариант) описывается следующими уравнениями (см. Т. Г. Нейлор, [29])

(6.4)

(6.5)

(6.6)

(6.7)

где:

Эндогенные переменные модели

C_t - потребление на интервале t,

I_t - инвестиции на интервале t,

G_t - правительственные расходы на интервале t,

Y_t - национальный доход на интервале t.

Экзогенные переменные

w_t, v_t - случайные величины с известным распределением (таким образом, известны их математическое ожидание и дисперсия).

Параметры

b - коэффициент акселерации,

c₁ - предельная склонность к потреблению на интервале t - 1, 0 < c₁ < 1

c₂ - предельная склонность к потреблению на интервале t - 2, 0 < c₂ < 1

g - коэффициент правительственных затрат.

Подставляя величины C_t, I_t, G_t из уравнений (6.4) - (6.6) в тождество (балансовое соотношение) (6.7), получим

или

(6.8)

где

Введем вектор . Тогда уравнения (6.4) - (6.6), (6.8) модели Самуэльсона - Хикса будут иметь вид

где

Пример 6.2. Многомерная модель динамики процентных ставок доходностей ценных бумаг

В таблице 6.1 приведены коэффициенты корреляции между ставками доходностей ценных бумаг казначейства США для различных сроков до погашения по данным 1995 г. (источник: Г. А. Медведев, 1999 г. [27]).

Таблица 6.1
Коэффициенты корреляции доходностей

Анализ данных таблицы показывает, что ставки доходностей ценных бумаг (облигаций) с различными сроками до погашения сильно коррелированы между собой. Это означает, что адекватные модели эволюции ставок доходностей различных ценных бумаг во времени должны учитывать их взаимосвязь. Для моделирования подобных взаимосвязанных процессов можно использовать модели многомерных временных рядов.

Обозначим - вектор - столбец отклонений ставок доходностей ценных бумаг с различными сроками погашения от их средних значений, здесь p - количество различных сроков погашения, соответствующих рассматриваемым ценным бумагам, - отклонение доходности ценной бумаги с j - ым сроком погашения от его среднего значения в момент времени t. Эволюцию вектора , (t=1,2,…) можно описать с помощью следующего векторного стохастического разностного уравнения

где - p - мерный вектор - столбец случайных величин; b - скалярный параметр; A - матрица параметров модели.

Пример 6.3. Модель прогнозирования процентных ставок и изменения денежной массы

Рассмотрим модель, разработанную Уеббом в 1984г. (см. "Эконометрика" под ред. И.И. Елисеевой, [35]) для прогнозирования процентных ставок и изменения (процентного) денежной массы. Простейший вариант модели имеет вид

где g(t) - процентная ставка, h(t) - объем денежной массы, a₁₁, a₁₂, a₂₁, a₂₂, c₁, c₂, - структурные параметры. Вводя вектор x(t) = [g(t),h(t)]^T, данную модель можно привести к виду (6.3) (наличие здесь констант c₁, c₂ не принципиально).

Отметим главную особенность рассмотренных моделей - состояние системы в момент времени t полностью определяется вектором x(t). В общей теории систем такой вектор называется вектором состояния системы. Говорят, что модель вида (6.3) описывает поведение процесса (системы) в пространстве состояний.

Понятие состояния - ключевое в современной теории динамических систем, оно применяется для описания, анализа, построения моделей многомерных систем (процессов) самой различной природы .

Приведем другие примеры использования понятия состояния для описания различных физических, технических, экономических систем:

1) Состояние электрических цепей характеризуется емкостными напряжениями и индуктивными токами.

2) Состояние любой механической системы определяется ее скоростью и пространственными координатами.

3) В модели управления посадкой самолета в качестве координат вектора состояния используются угол тангажа, скорость изменения угла тангажа, высота и скорость подъема.

4) В модели распределения Форрестера переменными состояния являются запасы, число служащих, невыполненные заказы, размеры капиталовложений, банковские балансы, заказы в пути, товары в процессе доставки и потребность в рабочей силе.

5) В моделях типа затраты - выпуск В. Леонтьева переменными состояния, по-существу, являются объемы продукции, выпускаемой отраслями.

6) В моделях инвестиционного портфеля в качестве переменных состояния взяты объемы вложений в различные финансовые активы.

В дальнейшем мы покажем, что используя методы пространства состояний можно строить, оценивать и анализировать более сложные (и более реалистичные) модели, нежели рассмотренные ранее статические регрессионные модели или динамические модели одномерных временных рядов.