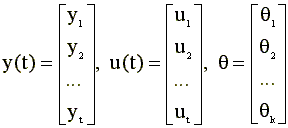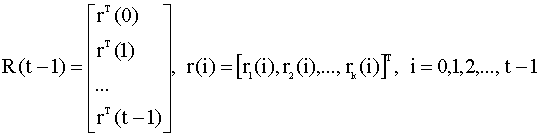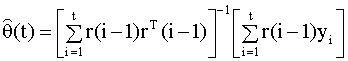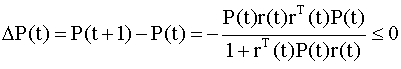|
6.2. Рекуррентный метод наименьших квадратов Рассматривая задачу оценивания параметров регрессионных моделей, мы предполагали, что количество наблюдений фиксировано и не изменяется. Однако, часто желательно обновлять оценки по мере поступления новых данных. Это особенно актуально при анализе временных рядов, так как в отличие от пространственных данных, где количество изучаемых объектов (скажем, торговых точек, см. пример 3.2), как правило, фиксировано и заранее известно, данные о поведении временного ряда могут поступать практически непрерывно и их количество неограниченно (как, например, ряды финансовых индексов). Если в этом случае использовать обычный (нерекуррентный) метод наименьших квадратов, то при поступлении каждого нового наблюдения необходимо будет повторять все вычисления, связанные с определением оценок, заново, причем размерность задачи будет все время возрастать. В связи с этим, рассмотрим рекуррентную версию метода наименьших квадратов, реализация которой не требует накопления всех прошлых данных и полного пересчета МНК - оценок. Кроме того, полученный результат будет служить базой для обоснования (вывода) уравнений фильтра Калмана, который является современным инструментом анализа многомерных временных рядов и широко используется на практике. Вывод уравнений рекуррентного МНК Рассмотрим модель множественной регрессии, которую запишем в виде
где векторы
и матрица регрессоров
Отметим, что с помощью моделей вида (6.9) на самом деле описывается более широкий класс регрессионных зависимостей, чем линейные статические модели множественной регрессии, которые мы рассматривали в главах 3, 4. Рассмотрим, например, модель вида
которая содержит авторегрессионную составляющую и экзогенные переменные z с учетом их запаздывания (напомним, что такие переменные называются лаговыми). Определим вектор регрессоров и вектор параметров Тогда, очевидно, уравнения (6.10) для совокупности наблюдений можно представить в виде (6.9). Оценка Для момента t + 1, после того, как будут получены новые значения измеряемых величин, можно записать
Вектор оценок параметров можно выразить как функцию последовательности векторов регрессоров r и наблюдений зависимой переменной y:
Введем матрицу W(t) и вектор q(t) следующим образом:
Тогда можно записать
Матрицу W(t) и вектор q(t) можно представить в рекуррентной форме
Используя (6.11) и (6.13), выразим оценку
Используя (6.12), выразим матрицу W(t) через W(t + 1) и подставим результат в (6.14). Получим или, после несложных преобразований, будем иметь
В уравнении (6.15) требуется определять обратную матрицу W-1(t + 1). Получим рекуррентное выражение для вычисления этой матрицы. Для этого используем лемму об обращении матриц, которая гласит (см. приложение), что для матриц A, B, C, D соответствующих (согласованных) размерностей имеет место равенство
при условии, что все обратные матрицы в выражении (6.16) существуют. Определим матрицу P(t + 1) следующим образом
Преобразуем выражение (6.17) с использованием (6.16). Положим Тогда, применяя лемму об обращении (6.16), запишем рекуррентное соотношение для определения матрицы P: Теперь можно записать уравнения рекуррентного метода наименьших квадратов:
где
вектор
матрица
Таким образом, одна итерация
рекуррентного МНК состоит в следующем.
До получения очередного наблюдения 1) вычисляем вектор K(t + 1) по формуле (6.20); 2) вычисляем прогноз наблюдения на один шаг по формуле (6.19); 3) определяем матрицу P(t + 1), используя рекуррентное соотношение (6.21). После получения наблюдения
вычисляем оценку В отличие от обычного МНК, при
использовании рекуррентного МНК не
требуется обращать матрицу, вместо
этого на каждом шаге производится
деление на скаляр Из структуры уравнения для
оценки (6.18)
следует, что после получения
очередного наблюдения, предыдущая
оценка корректируется путем
добавления ошибки
прогноза оценки на один шаг которая, по существу, совпадает с ранее полученным выражением (3.70) (см. гл. 3) для дисперсии прогноза индивидуального значения зависимой переменной. Инициализация алгоритма Для инициализации алгоритма
рекуррентного МНК необходимо
вычислить значение оценки для
некоторого момента t, начиная с
которого будет применяться
рекуррентная схема. Для этого, после
того, как будет накоплено достаточно
наблюдений и матрица W(t) станет
обратимой, полагаем P(t)=W-1(t) и
вычисляем оценку Суммируем основные свойства рекуррентного МНК. 1) Реализация рекуррентного МНК не требует обращения матриц. 2)
Разность между последовательными
значениями матриц P равна
то есть будет отрицательно полуопределенной матрицей. Это означает, что при увеличении количества наблюдений матрица P может только уменьшаться (за исключением случая, когда r(t) = 0 и наблюдения yt+1 не несут информации о параметрах 3) Если последовательность векторов регрессоров известна до того, как будут получены наблюдения регрессанда, то соответствующие последовательности матриц P и векторов K можно вычислить заранее. Замечание. Мы рассмотрели рекуррентный МНК как модификацию обычного МНК. Аналогично можно вывести рекуррентную версию обобщенного МНК. Рекуррентный МНК с экспоненциальным забыванием Рекуррентный МНК с экспоненциальным забыванием можно использовать, если предполагается, что оцениваемые параметры процесса медленно меняются. В этом случае прошлые данные не несут адекватной информации о параметрах, они искажают оценки, поскольку, по существу, относятся к модели с другими параметрами. Желательно отслеживать эти изменения по мере обработки поступающих наблюдений (или, как говорят, в реальном времени). В рекуррентном МНК с экспоненциальным забыванием рекуррентные соотношения для матрицы W и вектора q определяются следующим образом: где параметр
Замечание 1 Нетрудно видеть, что при Замечание 2 Если
|