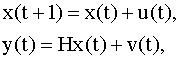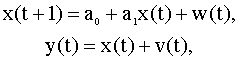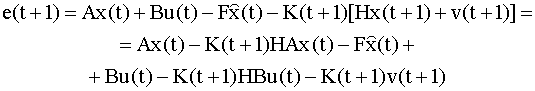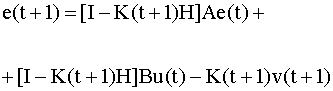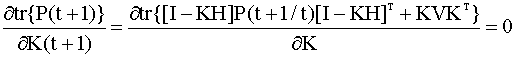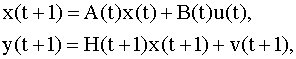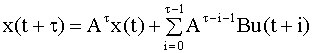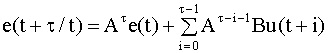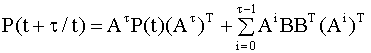Эконометрика

Глава 6. АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ

6.5. Фильтр Калмана и его применение для оценивания и прогнозирования не полностью наблюдаемых многомерных временных рядов

Модель неполностью наблюдаемого векторного случайного процесса

Выше (см. п.6.1) мы ввели понятие векторного (многомерного) случайного процесса (системы), причем модели типа авторегрессии являются частным случаем таких процессов. Построение моделей многомерных процессов основано на понятии вектора состояний и соответственно, пространства состояний системы (процесса). В общем случае процесс в пространстве состояний описывается следующими векторными разностными уравнениями

(6.29)

(6.30)

где H - известная матрица размера m x p, (в теории линейных систем эту матрицу называют матрицей наблюдений), вектор y(t) называется вектором наблюдений или выходом системы, v(t) - вектор независимых случайных шумов наблюдений с заданной матрицей ковариаций V и нулевым средним. Для простоты полагают также, что шумы модели и наблюдений некоррелированы между собой и с начальным состоянием x(0), кроме того, математическое ожидание M{x(0)}=0.

Основными чертами модели (6.29), (6.30) являются следующие:

1) эволюция во времени векторного процесса подчиняется уравнению (6.29);

2) наблюдению доступен не сам вектор состояния, характеризующий процесс, а некоторый другой вектор y(t), линейно связанный с вектором x(t) соотношением (6.30), причем наблюдения проводятся с ошибками.

Модель вида (6.29), (6.30) является естественным обобщением как моделей временных рядов, так и модели множественной линейной регрессии.

Пример 6.4

Модель авторегрессии. Процесс авторегрессии в пространстве состояний описывается уравнением (6.2). На практике часто наблюдения случайного ряда содержат ошибки. В этом случае в модели (6.2) вектор x неизвестен, но в качестве модели наблюдений можно принять модель (6.30) с единичной матрицей H.

Пример 6.5

Многомерная множественная регрессия. Модель многомерной регрессии можно представить в виде

(6.31)

где x(t) - вектор параметров регрессии, уравнение (6.31) означает, что этот вектор не зависит от времени; H - матрица регрессоров (не следует ее путать с матрицей наблюдений регрессоров, которая в обычном (не рекуррентном) МНК формируется из всех наблюдений регрессоров, по которым проводится оценивание параметров регрессии (ранее, в случае скалярных наблюдений y_t мы ее обозначали символом X)).

Пример 6.6

Многомерная регрессия с изменяющимися параметрами. Предыдущий пример можно обобщить на случай, когда параметры регрессионной модели - переменные величины. Моделью такой регрессии может служить модель вида

где флуктуации параметров регрессии x моделируются путем введения случайной компоненты (вектора) u.

Пример 6.7

Модель стохастической волатильности. При моделировании финансовых временных рядов (доходностей финансовых инструментов, в частности, обыкновенных акций), используются модели, в которых учитываются изменения дисперсий. Такие модели называются моделями волатильности. Рассмотрим так называемую модель стохастической волатильности (SV - модель), согласно которой доходность рискового актива z(t) (за вычетом средней доходности) описывается уравнениями

(6.32)

где a₀, a₁ - параметры модели, w(t), - белые шумы (последовательности некоррелированных случайных величин). Представим SV - модель в пространстве состояний. Введем вектор наблюдений

Тогда SV - модель (6.32), (6.33) в пространстве состояний имеет вид

где .

Вывод уравнений фильтра Калмана

Мощным инструментом анализа неполностью наблюдаемых векторных случайных процессов является фильтр Калмана.

Рассмотрим задачу оценивания вектора состояний системы (6.29) по последовательности наблюдений вида (6.30). Мы будем искать оценки, оптимальные в классе линейных по наблюдениям. Структура уравнений рекуррентного МНК позволяет предположить, что уравнения для оценок состояний модели (6.29), (6.30) должны иметь вид

(6.34)

где - p - вектор оценок, матрицы F и K подлежат определению. Матрицу F определим из условия несмещенности оценки. Запишем уравнение для ошибки оценки . Учитывая уравнения (6.29), (6.30) и (6.34), будем иметь

(6.35)

Положим F=[I - K(t + 1)H]A. Тогда уравнение (6.35) примет вид

(6.36)

Применяя к обеим частям уравнения (6.36) оператор математического ожидания, и полагая, что в начальный момент M{e(0)} = 0, получим M{e(t + 1)} = 0.

Таким образом, учитывая выражение для матрицы F, уравнение несмещенной оценки имеет вид

или, после несложных преобразований получим

(6.37)

Матрицу K определим из условия минимума суммарной по всем компонентам вектора состояний дисперсии ошибки оценки

здесь tr{ } означает след матрицы, - ковариационная матрица ошибки оценки.

Получим рекуррентное уравнение для матрицы P. Для этого умножим выражение, стоящее в правой части уравнения (6.36) на такое же, но только транспонированное и применим операцию взятия математического ожидания. Получим

(6.38)

здесь для простоты полагаем, что вектор шумов u имеет единичную матрицу ковариаций. Обозначим

- ковариационную матрицу ошибки прогноза оценки на один шаг

Для этой матрицы нетрудно получить выражение

(6.39)

С учетом (6.39), уравнение (6.38) запишем в виде

(6.40)

Условием минимума дисперсии будет

(6.41)

(в уравнении (6.41) аргумент у матрицы K для простоты опущен). Дифференцируя с использованием формул для производных по матричному аргументу (см. приложение), получим

откуда оптимальная матрица K равна

(6.42)

Заметим, что в выражении (6.42) обратная матрица всегда существует, поскольку матрица V - невырожденная. Уравнение (6.40) можно упростить, учитывая выражение (6.42). Действительно, нетрудно проверить, что при оптимальной матрице K вида (6.42) уравнение (6.40) примет вид

(6.43)

Уравнения (6.37), (6.39), (6.42), (6.43) называются уравнениями фильтра Калмана или просто фильтром Калмана (по имени его создателя), матрица K - коэффициентом усиления фильтра Калмана.

Замечание

Существует более десятка различных способов вывода уравнений фильтра Калмана. Мы выбрали возможно не самый строгий, но по-видимому, один из самых простых.

Реализация фильтра Калмана

Реализация алгоритма фильтрации требует проведения на каждой итерации следующих вычислений:

1) прогноз оценки на один шаг и вычисление ковариационной матрицы ошибки прогноза

(6.44)

(6.45)

2) вычисление коэффициента усиления фильтра

(6.46)

3) вычисление оценки

(6.47)

4) вычисление ковариационной матрицы ошибки оценки

(6.48)

Свойства фильтра Калмана

Суммируем основные свойства фильтра Калмана.

1) Так же как для рекуррентного метода наименьших квадратов, можно показать, что

то есть добавление новой информации, содержащейся в наблюдении y(t+1) может только уменьшить неопределенность в определении состояния.

2) Если векторные случайные последовательности u(t) и v(t) распределены по нормальному закону, то фильтр Калмана дает оптимальные оценки вектора состояний. При этом

Если шумы не гауссовские, оценки, получаемые с помощью фильтра Калмана будут оптимальными в классе линейных.

3) Наиболее важной особенностью (свойством) фильтра Калмана является его рекуррентная структура. Это позволяет получать оценки в реальном времени, по мере поступления наблюдений. При этом матрица усиления фильтра и матрица ковариаций ошибок оценок не зависят от наблюдений и их можно вычислить заранее, до поступления наблюдений. Это позволяет существенно сократить объем вычислений, проводимых в реальном времени.

4) В процессе вычисления оценок автоматически вычисляются характеристики точности этих оценок - матрицы ковариаций ошибок, диагональные элементы которых - дисперсии ошибок оценок компонент вектора состояний.

5) Рекуррентный метод наименьших квадратов, очевидно, является частным случаем фильтра Калмана, поскольку уравнения рекуррентного МНК совпадают с уравнениями фильтра Калмана для статической модели

Контроль расходимости фильтра Калмана

Один из способов контроля корректной работы фильтра заключается в следующем. На каждом шаге необходимо вычислять ковариационную матрицу ошибки предсказания на один шаг вектора наблюдений

Уравнение для ошибки имеет вид

Поскольку , ковариационная матрица ошибки равна

Диагональные элементы этой матрицы дают дисперсии ошибок прогноза компонент вектора наблюдений, а квадратные корни из дисперсий - стандартные отклонения. При нормальной работе фильтра ошибки прогноза редко будут превышать три стандартных отклонения. Если же ошибка растет, и часто превышает три стандартных отклонения, то это означает, что фильтр работает некорректно. В этом случае говорят, что фильтр расходится. Причинами этого явления могут быть следующие:

1) ошибки в моделировании динамики процесса - нарушение гипотезы линейности, не точный выбор матриц A, B, H;

2) некорректное задание ковариационных матриц шумов, V слишком мала;

3) некорректное задание начального значения - матрица P(0) слишком мала.

Обобщение на нестационарный случай

До сих пор мы предполагали, что матрицы A,B,H,V не зависят от времени, то есть рассматривали стационарные процессы (системы). Фильтр Калмана легко обобщить на случай нестационарных не полностью наблюдаемых процессов (систем), уравнения которых имеют вид

где ковариации шумов V(t) также зависят от времени. Для этого в уравнениях фильтра Калмана (6.44) - (6.48) достаточно указать явную зависимость матриц от времени.

Оценивание регрессии с изменяющимися параметрами

Фильтр Калмана можно использовать для оценивания модели множественной линейной регрессии с изменяющимися параметрами (см. пример 6.6, п. 6.5). В этом случае A = I, вектор параметров играет роль вектора состояний, а вектор шумов u моделирует возможные флуктуации параметров. Матрица H формируется из регрессоров, наблюдаемых до момента t - 1. Этот подход особенно эффективен, если имеется информация о степени возможных изменений параметров, которая позволяет задать матрицу ковариаций шумов u. Данный подход можно использовать как альтернативу рекуррентному МНК с забыванием. Его преимущество состоит в том, что выбор матрицы ковариаций вектора шумов дает больше возможностей для учета изменений параметров. Например, можно принять во внимание тот факт, что часть компонент вектора параметров постоянны (в матрице ковариаций им будут соответствовать нулевые диагональные элементы - дисперсии).

Прогнозирование

Наилучший в смысле минимума суммарной дисперсии ошибки прогноз вектора состояния на один шаг - это оценка вектора x(t + 1) по наблюдениям y(0), y(1), …, y(t), которая дается формулой

Ковариационная матрица ошибки прогноза на один шаг определяется уравнением (6.45).

Наилучший прогноз вектора x на шагов вперед относительно текущего момента времени t по наблюдениям вектора y до момента t включительно определяется по формуле

(6.49)

Получим уравнение для ковариационной матрицы ошибки прогноза на шагов

Прежде всего, выразим вектор состояния через x(t). Используя уравнение (6.29), запишем

(6.50)

Далее,

(6.51)

Обобщая формулы (6.50), (6.51), получаем

(6.52)

Учитывая уравнения (6.49) и (6.52), запишем выражение для ошибки прогноза

(6.53)

Используя уравнение (6.53) и учитывая, что последовательность векторов шумов u(t) некоррелированная с единичной ковариационной матрицей, нетрудно получить уравнение для ковариационной матрицы ошибки прогноза

(6.54)

Уравнение (6.54) можно переписать в более удобном виде

(6.55)

Диагональные элементы ковариационной матрицы определяют дисперсии ошибок прогноза отдельных компонент вектора состояний и служат характеристиками качества прогноза.

Уравнения (6.49), (6.55) можно представить в рекуррентной форме:

(6.56)

(6.57)

где , , .

Рекуррентные уравнения (6.56), (6.57) более удобны для вычислений.

Таким образом, алгоритм прогнозирования состоит из трех основных этапов:

1) Оценка вектора состояний процесса на момент времени t с использованием фильтра Калмана.

2) Вычисление прогноза по формуле (6.49) или рекуррентной формуле (6.56).

3) Одновременно по формуле (6.55) или, используя рекуррентное уравнение (6.57), вычисляют ковариационную матрицу ошибки прогноза, которая необходима для оценки качества прогноза.

Частный случай: прогнозирование полностью наблюдаемых случайных процессов

Если все компоненты вектора состояний x(t) многомерного процесса доступны наблюдению и при том без ошибок, то нет необходимости определять оценку вектора x(t) на момент t и в этом случае наилучший прогноз на шагов вперед относительно момента t вычисляется по формуле

(6.58)

Поскольку теперь P(t) - матрица, все элементы которой равны нулю (в момент t состояние процесса точно известно, так как измеряется без ошибок), то формула (6.55) для ковариационной матрицы ошибки прогноза примет вид

Для вычислений можно использовать также рекуррентные соотношения (6.56) и (6.57) с начальными условиями: , (здесь 0 - матрица с нулевыми элементами).

Замечание

Ранее (см. п. 6.1, уравнение (6.2)) мы получили представление уравнения авторегрессии в векторной форме (в пространстве состояний). Используя это представление, прогноз авторегрессионных процессов можно определять по формулам (6.58) или (6.56). Эти формулы являются обобщением полученных ранее (см. п. 5.4.5) формул для прогноза авторегрессионных процессов первого и второго порядков.